Chapter 12
Efficient Training Techniques
"Efficiency in AI training is not just about faster computations—it’s about smarter algorithms, better resource management, and innovative optimizations that push the boundaries of what’s possible." — Andrew Ng
Chapter 12 of LMVR delves into the techniques and strategies for efficiently training large language models using Rust. The chapter begins by emphasizing the importance of resource utilization, time, and cost in the training process, introducing key concepts such as parallelism, distributed training, and hardware acceleration. It covers the implementation of parallelism and concurrency in Rust, explores distributed training strategies, and discusses hardware-specific optimizations, including GPU and TPU integration. The chapter also examines the role of optimization algorithms, profiling, and real-time monitoring in enhancing training efficiency. Through practical implementations and case studies, the chapter provides a comprehensive guide to leveraging Rust’s features for scalable and efficient LLM training.
12.1. Introduction to Efficient Training
Efficient training of large language models (LLMs) is essential for optimizing resource utilization, reducing costs, and minimizing training time. As LLMs grow in size and complexity, the resources needed for training, including hardware, time, and energy, increase exponentially. Efficient training practices ensure that these resources are used strategically, balancing computational demands with budget and time constraints. This chapter introduces critical efficiency concepts such as parallelism, distributed training, and hardware acceleration, each of which plays a pivotal role in accelerating training processes without compromising model performance. In the context of Rust, which is optimized for speed and memory efficiency, implementing these techniques is particularly impactful, as Rust’s low-level control allows developers to maximize the hardware capabilities of GPUs, TPUs, or even multi-core CPUs, making it well-suited for high-performance training environments.

Figure 1: Optimization of LLM training.
Training LLMs requires handling vast datasets and intricate model architectures that are computationally intensive and demand high scalability. Parallelism, for instance, is essential in breaking down the training workload across multiple processors, allowing the model to be trained on different data subsets or portions of the model architecture simultaneously. In data parallelism, the same model is trained on separate data batches across multiple devices, synchronizing gradients after each step to ensure consistency. Model parallelism, by contrast, divides the model itself across devices, making it feasible to train models that exceed the memory capacity of a single device. Distributed training goes a step further, scaling across clusters of devices or nodes, essential for training the largest LLMs with billions of parameters. Rust’s memory management and concurrency support provide an edge in implementing these techniques, as they ensure reliable, low-latency communication between devices and efficient memory allocation for data parallelism and model partitioning.
There are inherent trade-offs between training speed and model accuracy. Reducing the time required for training often involves adjustments like smaller batch sizes or lower precision formats, which can introduce challenges in model convergence or degrade accuracy. However, efficient optimization techniques can help maintain a balance, allowing for high-speed training without sacrificing performance. Techniques like mixed-precision training, which uses both high- and low-precision data formats, reduce memory requirements and increase processing speed. Additionally, advanced gradient accumulation techniques allow effective large-batch training without needing extensive memory. By understanding these trade-offs, developers can tailor the training process to meet their specific requirements, optimizing for either speed, accuracy, or a balance of both.
Hardware-aware optimization is also critical in efficient training, especially for leveraging GPUs and TPUs. These processors are optimized for parallel computations, which is essential for matrix operations that underpin LLM training. Rust’s compatibility with CUDA for GPUs and XLA (Accelerated Linear Algebra) for TPUs provides a framework for harnessing these hardware accelerations effectively. By tailoring code to work within the architectural strengths of GPUs and TPUs, developers can ensure that each operation runs as efficiently as possible. This hardware-aware approach is especially valuable for LLMs, where extensive floating-point operations can benefit from parallelized execution and specialized data processing cores on GPUs and TPUs. Rust’s high-performance capabilities enable these computations to run smoothly, reducing overall training time and increasing throughput.
Setting up a Rust environment optimized for efficient LLM training involves selecting specific crates and configuring the toolchain for performance. This Rust code demonstrates a simple neural network training loop using the tch-rs crate, which provides bindings for PyTorch in Rust. The program creates a synthetic dataset, initializes a model with randomly generated weights, and trains it using the Adam optimizer over multiple epochs. The neural network model performs a matrix multiplication to make predictions, and the training loop minimizes the mean squared error loss by adjusting model weights through backpropagation.
[dependencies]
tokenizers = "0.20.1"
tch = "0.12.0"
use tch::{nn, nn::OptimizerConfig, Device, Tensor, Kind};
use std::error::Error;
// Dummy Model struct
struct Model {
weight: Tensor,
}
impl Model {
fn new(vs: &nn::Path, input_dim: i64, output_dim: i64) -> Self {
// Initialize model parameters with matching dimensions and mean/stdev
let weight = vs.randn("weight", &[input_dim, output_dim], 0.0, 1.0).set_requires_grad(true);
Self { weight }
}
fn forward(&self, inputs: &Tensor) -> Result<Tensor, Box<dyn Error>> {
// Forward function with correct dimensions
Ok(inputs.matmul(&self.weight))
}
fn backward(&self, loss: &Tensor) -> Result<(), Box<dyn Error>> {
// Calculate gradients
loss.backward();
Ok(())
}
}
// Synthetic Dataset struct
struct SyntheticDataset {
num_samples: usize,
input_dim: i64,
target_dim: i64,
}
impl SyntheticDataset {
fn new(num_samples: usize, input_dim: i64, target_dim: i64) -> Self {
Self {
num_samples,
input_dim,
target_dim,
}
}
fn batch(&self, batch_size: i64) -> Vec<Batch> {
(0..self.num_samples as i64 / batch_size)
.map(|_| {
// Generate random input and target tensors
let inputs = Tensor::randn(&[batch_size, self.input_dim], (Kind::Float, Device::Cpu));
let targets = Tensor::randn(&[batch_size, self.target_dim], (Kind::Float, Device::Cpu));
Batch { inputs, targets }
})
.collect()
}
}
// Struct to represent a batch of data
struct Batch {
inputs: Tensor,
targets: Tensor,
}
// Compute the Mean Squared Error loss
fn compute_loss(predictions: &Tensor, targets: &Tensor) -> Result<Tensor, Box<dyn Error>> {
let diff = predictions - targets;
let squared_diff = diff.pow_tensor_scalar(2); // Element-wise square
Ok(squared_diff.mean(Kind::Float)) // Compute the mean
}
fn main() -> Result<(), Box<dyn Error>> {
let vs = nn::VarStore::new(Device::Cpu); // VarStore for managing model parameters
let input_dim = 10;
let target_dim = 10;
let model = Model::new(&vs.root(), input_dim, target_dim);
let mut optimizer = nn::Adam::default().build(&vs, 1e-3)?; // Adam optimizer with learning rate 0.001
let dataset = SyntheticDataset::new(1000, input_dim, target_dim); // 1000 samples, input and target dim of 10
// Training loop with data parallelism (batch processing)
for epoch in 0..10 {
for batch in dataset.batch(32) {
let predictions = model.forward(&batch.inputs)?;
let loss = compute_loss(&predictions, &batch.targets)?;
// Backpropagation and optimization
model.backward(&loss)?;
optimizer.step();
optimizer.zero_grad();
}
println!("Epoch {} completed", epoch);
}
Ok(())
}
The code is structured around a custom Model struct that contains the network’s weights as a tensor, initialized to match the input and output dimensions. The Model struct has a forward method to compute predictions using matrix multiplication and a backward method to perform backpropagation. A SyntheticDataset struct generates random data batches for training, each with specified dimensions for inputs and targets. In the main training loop, the model makes predictions, computes the loss using mean squared error, and updates the weights based on gradients. The code iterates over multiple epochs, processing each batch and adjusting weights to minimize the error between predictions and targets.
Identifying bottlenecks in the training process is crucial for optimization. In Rust, developers can utilize profiling tools to identify areas where processing lags, such as inefficient memory allocation, I/O delays, or CPU-GPU communication overheads. For instance, profiling may reveal that data loading is slower than model computation, prompting the use of data caching or parallel data loading to reduce latency. Rust’s memory control allows developers to fine-tune data transfers and device synchronization, streamlining the training pipeline and ensuring consistent throughput across hardware.
Industry use cases of efficient training in Rust demonstrate the impact of these techniques on real-world applications. For example, companies developing language-based recommendation systems can benefit from accelerated training, as fast model updates allow them to incorporate recent user interactions and preferences into recommendations. In finance, where rapid analysis of market data is required, efficiently trained LLMs enable firms to generate timely insights, providing a competitive advantage. Trends in efficient training emphasize using mixed-precision, distributed parallelism, and custom hardware (e.g., TPUs), which are supported by Rust’s performance-optimized libraries and concurrency handling. By staying updated on these trends, developers can leverage Rust’s potential to achieve robust, efficient training pipelines for large-scale language models.
In conclusion, efficient training of LLMs involves a strategic approach that balances resource utilization, accuracy, and scalability. Rust’s low-level control and memory efficiency make it uniquely suited for developing high-performance, scalable training environments, from batch processing to complex parallelism across multiple devices. As the demand for LLMs continues to grow, efficient training practices will be essential for sustaining advancements in natural language processing, allowing companies to innovate while managing costs and resource constraints effectively.
12.2. Parallelism and Concurrency in Rust
Parallelism and concurrency are essential in accelerating the training of large models by enabling multiple computations to be processed simultaneously. Parallelism in model training involves splitting the data or model structure across multiple processing units, allowing computations to occur independently or concurrently. Concurrency, on the other hand, refers to managing multiple tasks within the same time frame, leveraging asynchronous operations to handle high-throughput workloads without overloading any single processor. Rust’s concurrency model, including its support for threads, async/await syntax, and parallel iterators, is particularly suited for such tasks due to its emphasis on safety, memory management, and low-level performance control.
Rust provides a range of tools for implementing parallelism, including threads, async/await, and dedicated libraries such as rayon and tokio. Threads enable parallel execution by creating separate processing pathways for tasks, while async/await is used to manage asynchronous tasks without blocking, which is crucial in training pipelines where I/O operations and computations need to occur without stalling the main process. The rayon crate, for example, simplifies parallel processing by offering parallel iterators that allow for efficient distribution of batch processing, an essential technique in data parallelism. Meanwhile, tokio provides a robust framework for asynchronous tasks, which is especially beneficial when managing networked or distributed training processes across multiple devices or nodes.
Data parallelism and model parallelism are two primary methods for parallelizing model training. In data parallelism, multiple copies of the same model are distributed across different devices or threads, and each copy processes a separate batch of data. The outputs are then aggregated, and gradients are synchronized to ensure consistency across model replicas. Mathematically, if a model $M$ is trained on data $D$, data parallelism distributes batches $D_1, D_2, \ldots, D_n$ across $n$ devices, where each device computes gradients independently as $\nabla M(D_i)$. These gradients are averaged across all devices to update model parameters, maintaining uniformity in the training process.
Model parallelism, by contrast, divides the model itself across multiple devices or threads, allowing different parts of the model to compute in parallel. For instance, in a deep neural network with layers $L_1, L_2, \ldots, L_k$, one device may process layers $L_1$ through $L_{k/2}$ while another processes $L_{k/2+1}$ through $L_k$. This technique is useful for training models that exceed the memory capacity of a single device, as it distributes the model’s storage and computational load. Rust’s ownership model and concurrency controls ensure memory safety and prevent data races, which are essential for parallelism where model components or data batches are processed simultaneously.
Rayon is a data parallelism library for Rust that enables easy and efficient parallel processing using high-level abstractions. By leveraging Rayon, developers can transform standard Rust iterators into parallel iterators, which automatically distribute tasks across available CPU cores. This process allows applications to speed up tasks that can be processed concurrently, like batch computations, without manually handling thread management, locking, or load balancing. Rayon is particularly useful in computational workloads, such as machine learning, where tasks can often be split across data chunks and processed in parallel.
The rayon crate simplifies data parallelism by enabling parallel iterators, which automatically distribute tasks across available threads. This feature is especially useful in batch processing, where data can be divided into smaller subsets and processed in parallel, speeding up the training loop. The following Rust code demonstrates data parallelism using rayon, where each batch in the dataset is processed concurrently to accelerate training:
use ndarray::{Array, Array1, Array2, ArrayView2, Axis};
use ndarray_rand::rand_distr::Uniform;
use ndarray_rand::RandomExt;
use rayon::prelude::*; // Import Rayon for parallel iterators
use std::sync::Mutex; // Import Mutex to manage shared access
use std::time::Instant;
// Hyperparameters
const INPUT_SIZE: usize = 10;
const HIDDEN_SIZE: usize = 5;
const OUTPUT_SIZE: usize = 1;
const BATCH_SIZE: usize = 64;
const LEARNING_RATE: f32 = 0.01;
const EPOCHS: usize = 100;
// Neural Network struct
struct NeuralNetwork {
w1: Array2<f32>,
w2: Array2<f32>,
b1: Array1<f32>,
b2: Array1<f32>,
}
impl NeuralNetwork {
fn new() -> Self {
let w1 = Array::random((INPUT_SIZE, HIDDEN_SIZE), Uniform::new(-1.0, 1.0));
let w2 = Array::random((HIDDEN_SIZE, OUTPUT_SIZE), Uniform::new(-1.0, 1.0));
let b1 = Array::zeros(HIDDEN_SIZE);
let b2 = Array::zeros(OUTPUT_SIZE);
Self { w1, w2, b1, b2 }
}
fn forward(&self, x: ArrayView2<f32>) -> Array2<f32> {
let hidden = (x.dot(&self.w1) + &self.b1).map(|v| v.max(0.0)); // ReLU activation
hidden.dot(&self.w2) + &self.b2 // Output layer (no activation for regression)
}
fn backward(&mut self, x: ArrayView2<f32>, y: ArrayView2<f32>, output: ArrayView2<f32>) {
let error = &output - &y;
let hidden = (x.dot(&self.w1) + &self.b1).map(|v| v.max(0.0)); // Recalculate hidden layer
let hidden_grad = hidden.map(|&v| if v > 0.0 { 1.0 } else { 0.0 }); // Derivative of ReLU
// Calculate gradients for the second layer
let d_w2 = hidden.t().dot(&error) / x.shape()[0] as f32;
let d_b2 = error.sum_axis(Axis(0)) / x.shape()[0] as f32;
// Backpropagate the error to the first layer
let d_hidden = error.dot(&self.w2.t()) * &hidden_grad;
let d_w1 = x.t().dot(&d_hidden) / x.shape()[0] as f32;
let d_b1 = d_hidden.sum_axis(Axis(0)) / x.shape()[0] as f32;
// Update weights and biases by scaling gradients with LEARNING_RATE
self.w2 -= &(d_w2 * LEARNING_RATE);
self.b2 -= &(d_b2 * LEARNING_RATE);
self.w1 -= &(d_w1 * LEARNING_RATE);
self.b1 -= &(d_b1 * LEARNING_RATE);
}
}
// Generate synthetic data
fn generate_synthetic_data(n: usize) -> (Array2<f32>, Array2<f32>) {
let x = Array::random((n, INPUT_SIZE), Uniform::new(-1.0, 1.0));
let y = x.sum_axis(Axis(1)).to_shape((n, OUTPUT_SIZE)).unwrap().to_owned(); // Target is sum of inputs
(x, y)
}
// Sequential training
fn train_sequential(nn: &mut NeuralNetwork, x_train: &Array2<f32>, y_train: &Array2<f32>) {
for epoch in 0..EPOCHS {
for (x_batch, y_batch) in x_train
.axis_chunks_iter(Axis(0), BATCH_SIZE)
.zip(y_train.axis_chunks_iter(Axis(0), BATCH_SIZE))
{
let output = nn.forward(x_batch.view());
nn.backward(x_batch.view(), y_batch.view(), output.view());
}
let output = nn.forward(x_train.view());
let loss = (&output - y_train).mapv(|x| x.powi(2)).mean().unwrap();
println!("Sequential Epoch: {}, Loss: {:.4}", epoch, loss);
}
}
// Parallel training with Rayon
fn train_parallel(nn: &Mutex<NeuralNetwork>, x_train: &Array2<f32>, y_train: &Array2<f32>) {
for epoch in 0..EPOCHS {
let batches: Vec<_> = x_train
.axis_chunks_iter(Axis(0), BATCH_SIZE)
.zip(y_train.axis_chunks_iter(Axis(0), BATCH_SIZE))
.collect();
// Process each batch in parallel using Rayon
batches.par_iter().for_each(|(x_batch, y_batch)| {
let output;
{
// Lock the network for forward pass and backward pass
let mut nn_locked = nn.lock().unwrap();
output = nn_locked.forward(x_batch.view());
nn_locked.backward(x_batch.view(), y_batch.view(), output.view());
}
});
// Evaluate loss
let nn_locked = nn.lock().unwrap(); // Lock once to evaluate the loss
let output = nn_locked.forward(x_train.view());
let loss = (&output - y_train).mapv(|x| x.powi(2)).mean().unwrap();
println!("Parallel Epoch: {}, Loss: {:.4}", epoch, loss);
}
}
fn main() {
let (x_train, y_train) = generate_synthetic_data(1000);
// Sequential training
let mut nn_sequential = NeuralNetwork::new();
let start_sequential = Instant::now();
train_sequential(&mut nn_sequential, &x_train, &y_train);
let duration_sequential = start_sequential.elapsed();
println!(
"\nSequential training took: {:.2?} seconds",
duration_sequential
);
// Parallel training with Rayon
let nn_parallel = Mutex::new(NeuralNetwork::new());
let start_parallel = Instant::now();
train_parallel(&nn_parallel, &x_train, &y_train);
let duration_parallel = start_parallel.elapsed();
println!(
"\nParallel training took: {:.2?} seconds",
duration_parallel
);
// Compare the performance
println!(
"\nSpeedup: {:.2}x",
duration_sequential.as_secs_f64() / duration_parallel.as_secs_f64()
);
}
In the code, we first define a simple neural network and train it both sequentially and in parallel using Rayon for comparison. We generate synthetic data as input and target values for training, and then create two training functions: train_sequential for sequential training and train_parallel for parallelized training with Rayon. The train_parallel function uses Rayon’s par_iter to process each batch concurrently by splitting the data into smaller, independent subsets. We use a Mutex to safely share the neural network instance across threads during the parallel update process. Both training versions are timed using Instant to measure and compare their performances, with a final speedup calculation to quantify the improvement achieved with parallelism.
Model parallelism is an essential approach for training large neural networks that cannot fit entirely on a single device. In model parallelism, different parts of the model are distributed across multiple devices (e.g., CPUs or GPUs), each handling a subset of computations. This method contrasts with data parallelism, where the entire model is replicated on each device, and each processes a subset of the data. In Rust, model parallelism can be implemented using the standard std::thread library, allowing each thread to independently process a model layer or group of operations. By dividing the model's computations among threads, we can leverage multi-core processors to achieve better resource utilization and potentially faster training times for large models.
use ndarray::{Array, Array2, Axis, s};
use ndarray_rand::rand_distr::Uniform;
use ndarray_rand::RandomExt;
use std::sync::{Arc, Mutex};
use std::thread;
use std::time::Instant;
// Define hyperparameters
const INPUT_SIZE: usize = 10;
const HIDDEN_SIZE: usize = 64;
const OUTPUT_SIZE: usize = 1;
const LEARNING_RATE: f32 = 0.01;
const BATCH_SIZE: usize = 64;
const EPOCHS: usize = 10;
// Define a basic neural network structure
struct NeuralNetwork {
w1: Arc<Mutex<Array2<f32>>>,
b1: Arc<Mutex<Array2<f32>>>,
w2: Arc<Mutex<Array2<f32>>>,
b2: Arc<Mutex<Array2<f32>>>,
}
impl NeuralNetwork {
fn new() -> Self {
let w1 = Array::random((INPUT_SIZE, HIDDEN_SIZE), Uniform::new(-0.5, 0.5));
let b1 = Array::zeros((1, HIDDEN_SIZE));
let w2 = Array::random((HIDDEN_SIZE, OUTPUT_SIZE), Uniform::new(-0.5, 0.5));
let b2 = Array::zeros((1, OUTPUT_SIZE));
NeuralNetwork {
w1: Arc::new(Mutex::new(w1)),
b1: Arc::new(Mutex::new(b1)),
w2: Arc::new(Mutex::new(w2)),
b2: Arc::new(Mutex::new(b2)),
}
}
fn forward_layer1(&self, x: &Array2<f32>) -> Array2<f32> {
let w1 = self.w1.lock().unwrap();
let b1 = self.b1.lock().unwrap();
(x.dot(&*w1) + &*b1).mapv(f32::tanh)
}
fn forward_layer2(&self, h1: &Array2<f32>) -> Array2<f32> {
let w2 = self.w2.lock().unwrap();
let b2 = self.b2.lock().unwrap();
h1.dot(&*w2) + &*b2
}
fn backward_layer1(&self, d_w1: Array2<f32>, d_b1: Array2<f32>) {
let mut w1 = self.w1.lock().unwrap();
let mut b1 = self.b1.lock().unwrap();
*w1 -= &(d_w1 * LEARNING_RATE);
*b1 -= &(d_b1 * LEARNING_RATE);
}
fn backward_layer2(&self, d_w2: Array2<f32>, d_b2: Array2<f32>) {
let mut w2 = self.w2.lock().unwrap();
let mut b2 = self.b2.lock().unwrap();
*w2 -= &(d_w2 * LEARNING_RATE);
*b2 -= &(d_b2 * LEARNING_RATE);
}
}
// Synthetic data generation
fn generate_synthetic_data(n: usize) -> (Array2<f32>, Array2<f32>) {
let x = Array::random((n, INPUT_SIZE), Uniform::new(0., 1.));
let y = x.sum_axis(Axis(1)).to_shape((n, OUTPUT_SIZE)).unwrap().to_owned();
(x, y)
}
// Model parallel training function
fn train_model_parallel(nn: Arc<NeuralNetwork>, x: &Array2<f32>, y: &Array2<f32>) {
let h1 = {
let nn = nn.clone();
nn.forward_layer1(x)
};
let output = {
let nn = nn.clone();
nn.forward_layer2(&h1)
};
// Calculate gradients
let error = &output - y;
let d_w2 = h1.t().dot(&error).to_owned();
let d_b2 = error.sum_axis(Axis(0)).to_shape((1, OUTPUT_SIZE)).unwrap().to_owned();
// Split updates across threads for model parallelism
let nn1 = nn.clone();
let nn2 = nn.clone();
let x_clone = x.clone();
let backward1_handle = thread::spawn(move || {
let d_hidden = error.dot(&nn2.w2.lock().unwrap().t()) * (1. - h1.mapv(|v| v.powi(2)));
let d_w1 = x_clone.t().dot(&d_hidden).to_owned();
let d_b1 = d_hidden.sum_axis(Axis(0)).to_shape((1, HIDDEN_SIZE)).unwrap().to_owned();
nn2.backward_layer1(d_w1, d_b1);
});
nn1.backward_layer2(d_w2, d_b2);
backward1_handle.join().unwrap();
}
fn main() {
let (x, y) = generate_synthetic_data(1000);
let nn = Arc::new(NeuralNetwork::new());
let start = Instant::now();
for _ in 0..EPOCHS {
for i in (0..x.len_of(Axis(0))).step_by(BATCH_SIZE) {
let end_idx = std::cmp::min(i + BATCH_SIZE, x.len_of(Axis(0))); // Ensure end index doesn't exceed array length
let x_batch = x.slice(s![i..end_idx, ..]).to_owned();
let y_batch = y.slice(s![i..end_idx, ..]).to_owned();
train_model_parallel(nn.clone(), &x_batch, &y_batch);
}
}
println!("Training completed in {:?}", start.elapsed());
}
The code demonstrates a basic implementation of model parallelism in Rust using threads. A simple neural network with two layers is defined, with weights and biases stored as shared resources across threads. Each epoch, the input batch is passed through two separate forward layers in sequence. The error is then computed to perform backpropagation, where gradients for each layer are computed independently. To enable parallelism, the gradients for the first and second layers are computed in separate threads using std::thread::spawn, updating the respective weights and biases asynchronously. This setup distributes the model computations for each layer across threads, allowing each part of the model to be trained independently. The main function generates synthetic data, iterates through epochs and batches, and applies model parallelism during training. Finally, it measures and outputs the total training time.
Implementing parallelism in Rust directly impacts training time and resource utilization. By distributing data and model components across multiple threads or devices, training processes can complete more rapidly without overburdening any single processor. Profiling tools like perf or tokio-tracing can be used to analyze thread activity, identify bottlenecks, and assess the impact of parallelism on training. Metrics such as CPU and GPU utilization, latency, and memory consumption are crucial indicators for determining how efficiently the system is using resources. Identifying these bottlenecks helps refine the parallelism strategy, optimizing performance further through load balancing or refining batch sizes.
Industry applications of parallelism in training have grown extensively, with fields like autonomous vehicles and finance benefiting from reduced training times. In autonomous systems, rapid model updates are crucial for integrating new sensor data and enhancing real-time decision-making. Similarly, in finance, parallelism enables faster training on large transaction datasets, which is essential for fraud detection and predictive analytics. Emerging trends include hybrid parallelism strategies, which combine data and model parallelism to optimize for large-scale distributed training, an area where Rust’s performance and concurrency capabilities can be fully leveraged.
In conclusion, parallelism and concurrency are transformative in training large models, enabling faster, more efficient use of hardware resources. Rust’s robust concurrency model, combined with crates like rayon and tokio, provides a powerful framework for implementing parallelism safely and effectively. By distributing both data and model components across multiple threads or devices, Rust-based systems can achieve high-performance training, pushing the boundaries of scalability and efficiency in large language models and other complex AI systems.
12.3. Distributed Training Techniques
Distributed training has become a cornerstone for scaling large language models (LLMs) to handle expansive datasets and highly complex architectures. By distributing the workload across multiple devices or nodes, distributed training enables substantial acceleration of model training and allows for larger models that would be challenging to train on a single machine. Key strategies in distributed training include data parallelism, model parallelism, and pipeline parallelism, each with specific use cases and performance implications. Data parallelism, for instance, divides the dataset across nodes with each node holding a replica of the model, while model parallelism splits the model itself, allowing each node to process a different part of the architecture. Pipeline parallelism chains parts of the model across nodes, processing data sequentially in a pipeline fashion, enabling efficient memory and computational load distribution.
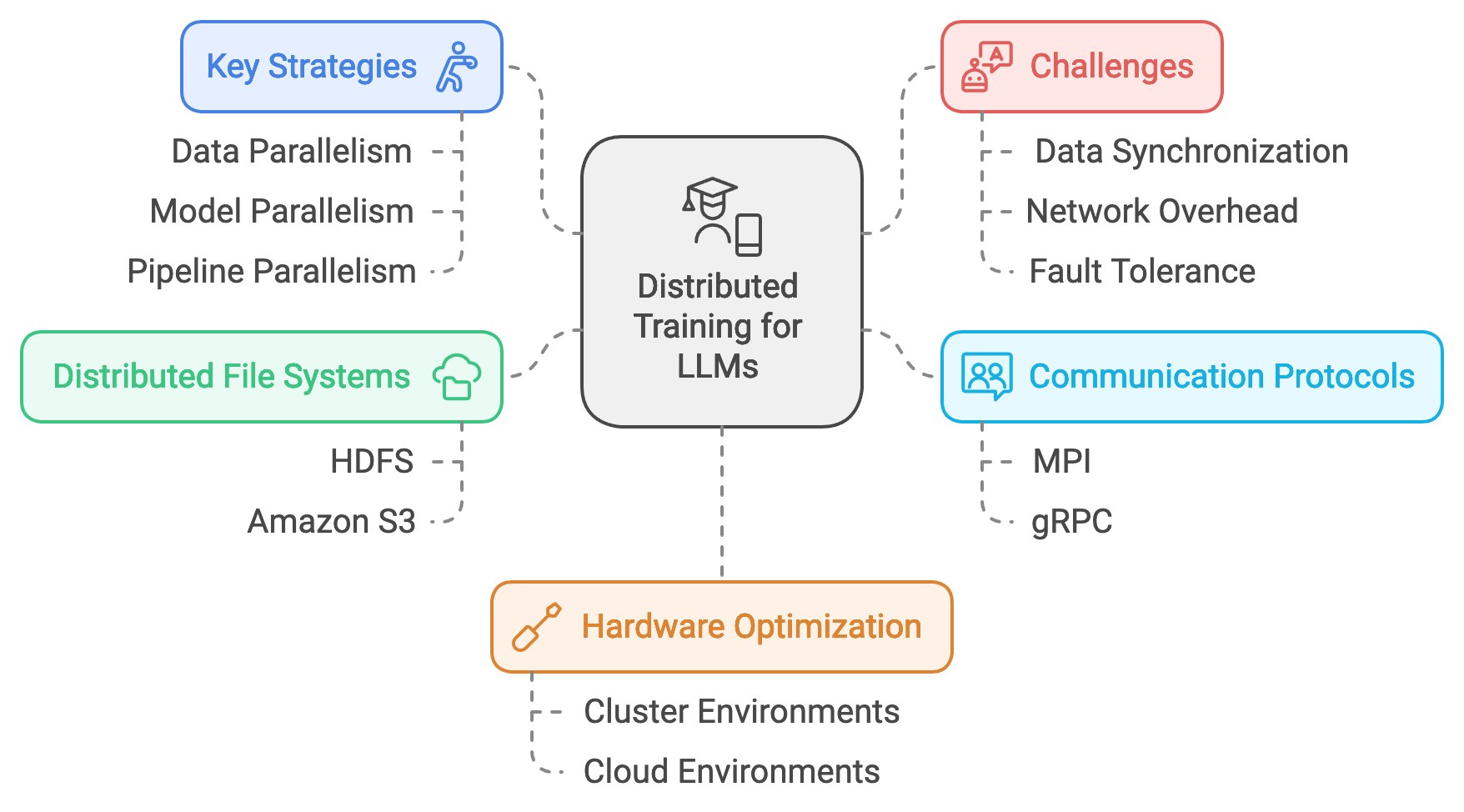
Figure 2: Distributed training strategy for LLMs.
Communication protocols and tools are central to distributed training, as nodes need to synchronize data and gradients during training. MPI (Message Passing Interface) is a widely-used protocol that facilitates communication across nodes, managing data transmission effectively in high-performance environments. Similarly, gRPC (Google Remote Procedure Call) is commonly used in cloud-based settings, enabling fast and reliable communication between nodes across distributed clusters. These tools allow for data sharing, synchronization, and collective operations like gradient averaging, essential for maintaining consistency during distributed training.
Distributed training introduces several challenges, including data synchronization, network communication overhead, and fault tolerance. Data synchronization ensures that updates from each node are aggregated consistently, especially when using data parallelism, where gradient accumulation must be precise across replicas to avoid inconsistencies. Network communication overhead can become significant as model size and node count increase, potentially slowing down training. Strategies such as gradient compression and asynchronous updates can mitigate some of these issues by reducing the amount of data transmitted or allowing nodes to operate independently without waiting for synchronization. Fault tolerance is another key consideration in distributed setups, as node failures can disrupt training. To address this, redundancy strategies and checkpointing ensure that training can resume from a recent state without loss of progress.
Distributed file systems and data sharding play a crucial role in managing large datasets across multiple nodes. Distributed file systems, such as Hadoop Distributed File System (HDFS) or Amazon S3, provide scalable storage solutions that allow nodes to access data concurrently, reducing bottlenecks associated with I/O operations. Data sharding divides the dataset into smaller, manageable pieces stored across nodes, enhancing read and write efficiency and ensuring that data is readily available to each node. This setup is essential for handling large datasets typical in LLM training, where data must be processed quickly and efficiently to keep up with the computational demands of distributed training.
Optimizing distributed training for different hardware setups requires consideration of hardware-specific configurations and performance constraints. In cluster environments, low-latency, high-bandwidth networks are critical, as nodes communicate frequently during synchronization. Distributed training in cloud environments, meanwhile, benefits from elasticity, where computational resources scale dynamically based on training demands. Selecting the right configuration for distributed training depends on factors such as the model size, the dataset, and the desired level of scalability. For example, hardware setups with high inter-node communication costs may benefit more from asynchronous updates, reducing the dependency on synchronization.
In deep learning, parallelism is crucial for efficiently training models, especially when handling large datasets or complex models that demand significant computational resources. Two primary types of parallelism used in neural networks are data parallelism and model parallelism. Data parallelism involves splitting data across multiple devices or processing units, allowing each to perform computations independently before synchronizing the results. This approach works well when the model fits entirely within each device's memory. However, model parallelism becomes essential when the model is too large to fit on a single device, especially for layers with a vast number of parameters.
In model parallelism, different parts of the model are distributed across separate devices or processing units. Each part computes a distinct subset of the model’s operations, and intermediate results are passed between them. This allows for the distribution of a model’s components across multiple resources, alleviating memory constraints on a single device. Although model parallelism can introduce communication overhead when transferring data between different parts of the model, it is often the only feasible way to train massive neural networks that exceed the capacity of a single device’s memory.
use ndarray::{Array, Array2, Axis, s};
use ndarray_rand::rand_distr::Uniform;
use ndarray_rand::RandomExt;
use std::sync::{Arc, Mutex};
use std::thread;
use std::time::Instant;
// Define hyperparameters
const INPUT_SIZE: usize = 10;
const HIDDEN_SIZE: usize = 64;
const OUTPUT_SIZE: usize = 1;
const LEARNING_RATE: f32 = 0.01;
const BATCH_SIZE: usize = 64;
const EPOCHS: usize = 10;
// Define a basic neural network structure
struct NeuralNetwork {
w1: Arc<Mutex<Array2<f32>>>,
b1: Arc<Mutex<Array2<f32>>>,
w2: Arc<Mutex<Array2<f32>>>,
b2: Arc<Mutex<Array2<f32>>>,
}
impl NeuralNetwork {
fn new() -> Self {
let w1 = Array::random((INPUT_SIZE, HIDDEN_SIZE), Uniform::new(-0.5, 0.5));
let b1 = Array::zeros((1, HIDDEN_SIZE));
let w2 = Array::random((HIDDEN_SIZE, OUTPUT_SIZE), Uniform::new(-0.5, 0.5));
let b2 = Array::zeros((1, OUTPUT_SIZE));
NeuralNetwork {
w1: Arc::new(Mutex::new(w1)),
b1: Arc::new(Mutex::new(b1)),
w2: Arc::new(Mutex::new(w2)),
b2: Arc::new(Mutex::new(b2)),
}
}
fn forward_layer1(&self, x: &Array2<f32>) -> Array2<f32> {
let w1 = self.w1.lock().unwrap();
let b1 = self.b1.lock().unwrap();
(x.dot(&*w1) + &*b1).mapv(f32::tanh)
}
fn forward_layer2(&self, h1: &Array2<f32>) -> Array2<f32> {
let w2 = self.w2.lock().unwrap();
let b2 = self.b2.lock().unwrap();
h1.dot(&*w2) + &*b2
}
fn backward_layer1(&self, d_w1: Array2<f32>, d_b1: Array2<f32>) {
let mut w1 = self.w1.lock().unwrap();
let mut b1 = self.b1.lock().unwrap();
*w1 -= &(d_w1 * LEARNING_RATE);
*b1 -= &(d_b1 * LEARNING_RATE);
}
fn backward_layer2(&self, d_w2: Array2<f32>, d_b2: Array2<f32>) {
let mut w2 = self.w2.lock().unwrap();
let mut b2 = self.b2.lock().unwrap();
*w2 -= &(d_w2 * LEARNING_RATE);
*b2 -= &(d_b2 * LEARNING_RATE);
}
}
// Synthetic data generation
fn generate_synthetic_data(n: usize) -> (Array2<f32>, Array2<f32>) {
let x = Array::random((n, INPUT_SIZE), Uniform::new(0., 1.));
let y = x.sum_axis(Axis(1)).to_shape((n, OUTPUT_SIZE)).unwrap().to_owned();
(x, y)
}
// Model parallel training function
fn train_model_parallel(nn: Arc<NeuralNetwork>, x: &Array2<f32>, y: &Array2<f32>) {
let h1 = {
let nn = nn.clone();
nn.forward_layer1(x)
};
let output = {
let nn = nn.clone();
nn.forward_layer2(&h1)
};
// Calculate gradients
let error = &output - y;
let d_w2 = h1.t().dot(&error).to_owned();
let d_b2 = error.sum_axis(Axis(0)).to_shape((1, OUTPUT_SIZE)).unwrap().to_owned();
// Split updates across threads for model parallelism
let nn1 = nn.clone();
let nn2 = nn.clone();
let x_clone = x.clone();
let backward1_handle = thread::spawn(move || {
let d_hidden = error.dot(&nn2.w2.lock().unwrap().t()) * (1. - h1.mapv(|v| v.powi(2)));
let d_w1 = x_clone.t().dot(&d_hidden).to_owned();
let d_b1 = d_hidden.sum_axis(Axis(0)).to_shape((1, HIDDEN_SIZE)).unwrap().to_owned();
nn2.backward_layer1(d_w1, d_b1);
});
nn1.backward_layer2(d_w2, d_b2);
backward1_handle.join().unwrap();
}
fn main() {
let (x, y) = generate_synthetic_data(1000);
let nn = Arc::new(NeuralNetwork::new());
let start = Instant::now();
for epoch in 0..EPOCHS {
for i in (0..x.len_of(Axis(0))).step_by(BATCH_SIZE) {
let end_idx = std::cmp::min(i + BATCH_SIZE, x.len_of(Axis(0))); // Ensure end index doesn't exceed array length
let x_batch = x.slice(s![i..end_idx, ..]).to_owned();
let y_batch = y.slice(s![i..end_idx, ..]).to_owned();
train_model_parallel(nn.clone(), &x_batch, &y_batch);
}
println!("Epoch {} completed", epoch + 1);
}
println!("Training completed in {:?}", start.elapsed());
}
The code above implements basic model parallelism by dividing the forward and backward passes into separate threads. It defines a simple two-layer neural network with weights and biases encapsulated in an Arc structure for safe multi-threaded access. The first layer's computations (forward_layer1) run independently, producing intermediate results (h1) for the second layer. Gradients are then computed, and the updates are split across two threads. One thread handles the weight and bias updates for the second layer (backward_layer2), while another thread updates the parameters for the first layer (backward_layer1). This allows both layers' gradients to be calculated and applied in parallel, demonstrating a simplified model-parallel training setup in Rust.
Experimenting with different distributed training strategies provides insights into their impact on training performance. For example, synchronous updates, where nodes synchronize gradients after each step, ensure consistent model updates but can introduce delays in large setups with significant communication overhead. Asynchronous updates, by contrast, allow nodes to update their models independently, reducing synchronization delay but introducing potential inconsistencies in model updates. These strategies can be tested and compared in Rust, with performance metrics such as latency, accuracy, and throughput providing feedback on the most suitable approach for a given environment.
Deploying a distributed training pipeline on a cloud-based cluster allows for scalability and evaluation of the training setup in a production environment. Cloud platforms, such as AWS and Google Cloud, provide managed solutions for distributed training, with support for GPU and TPU clusters that can be dynamically scaled based on demand. By deploying the Rust-based distributed training pipeline on a cloud cluster, developers can evaluate its scalability and efficiency, optimizing resource allocation based on the computational needs of the model. Monitoring tools, such as Prometheus or Grafana, track resource utilization and latency, allowing fine-tuning of distributed strategies to achieve optimal performance.
Distributed training techniques are transformative in industries where rapid model updates and large-scale training are essential. In personalized content recommendations, for example, distributed training enables frequent model updates based on recent user interactions, enhancing recommendation relevance. In autonomous systems, where models require constant retraining on new sensor data, distributed training allows companies to scale effectively, accommodating the large datasets needed for real-time decision-making. Trends in distributed training focus on hybrid parallelism, combining data, model, and pipeline parallelism to optimize resource usage, and leveraging cloud infrastructure to support elastic scalability, areas where Rust’s performance and control offer distinct advantages.
In summary, distributed training techniques provide the foundation for scaling LLMs effectively, allowing them to leverage vast datasets and complex architectures. Rust’s concurrency support and low-level control make it particularly suitable for implementing distributed training, from data synchronization to communication management. By applying distributed file systems, data sharding, and cloud-based deployment, Rust-based distributed training pipelines can achieve high efficiency, reliability, and scalability, positioning them for advanced, production-grade machine learning applications.
12.4. Hardware Acceleration and Optimization
Hardware acceleration plays an essential role in training large language models (LLMs), where GPUs, TPUs, and custom accelerators provide the computational power needed for intensive matrix operations and parallelized data processing. Accelerators enable faster computations by leveraging specialized cores optimized for linear algebra operations common in neural network training. For example, GPUs excel in processing large batches of data simultaneously, while TPUs, designed explicitly for tensor operations, offer even higher efficiency for specific machine learning tasks. To harness this power, hardware-aware optimization techniques like kernel fusion, mixed precision training, and memory management are applied to maximize resource utilization and minimize bottlenecks in training pipelines. Rust’s ecosystem, with bindings to low-level libraries like CUDA for NVIDIA GPUs and ROCm for AMD GPUs, facilitates these optimizations, providing developers with the control needed to configure high-performance, hardware-optimized training.
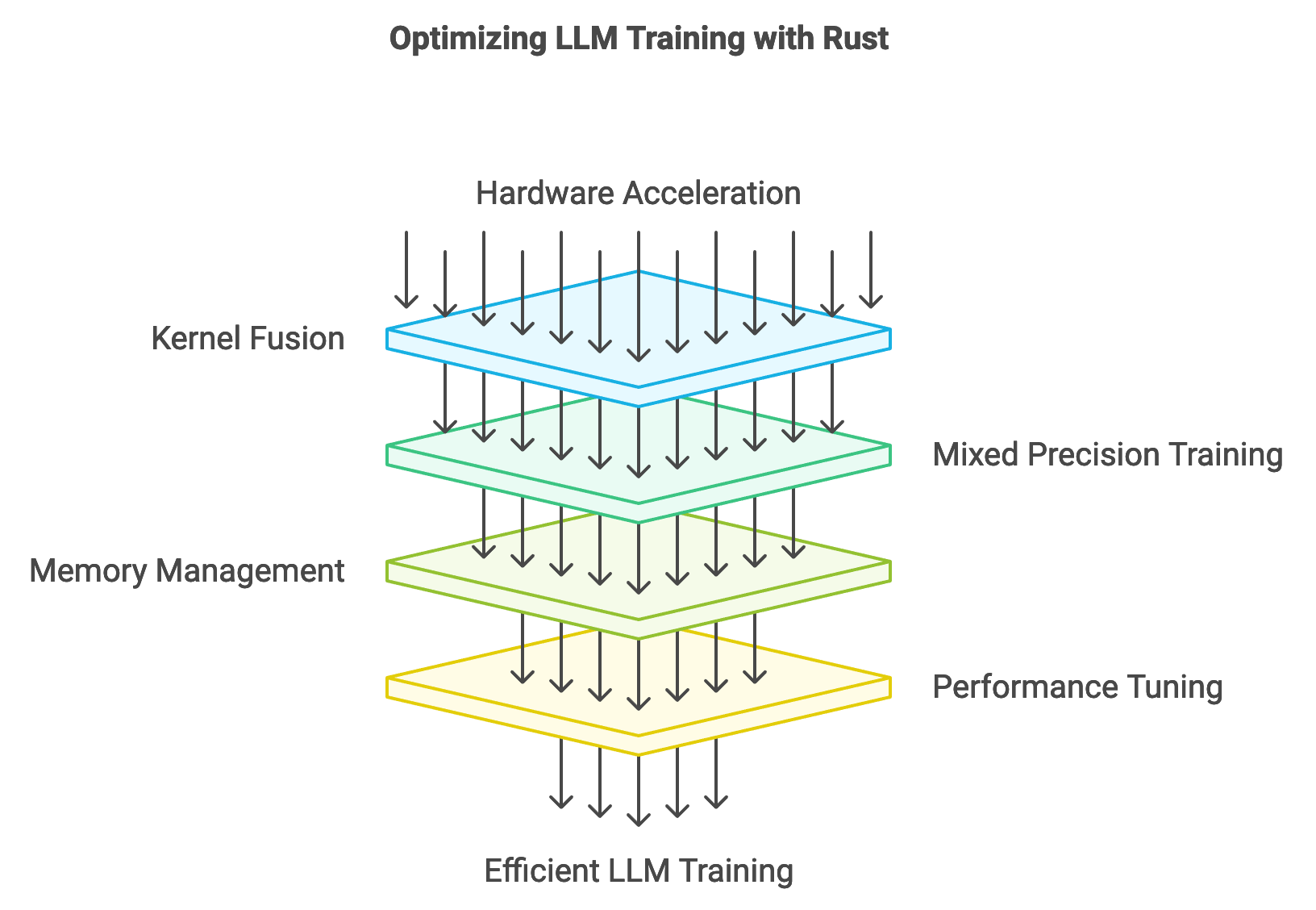
Figure 3: Hardware acceleration strategy for LLM training.
Kernel fusion is a critical technique that combines multiple computation steps into a single kernel, reducing the number of memory access points and improving data flow within the processor. For example, consider two operations: element-wise addition and ReLU activation. By fusing these into a single kernel, the data only needs to be loaded and stored once, reducing memory access latency. Mathematically, kernel fusion can be represented as $Y = \text{ReLU}(X + W)$ where $X$ and $W$ are tensors. Instead of computing $Z = X + W$ followed by $Y = \text{ReLU}(Z)$, kernel fusion performs both operations in one pass. This is particularly advantageous on GPUs, where minimizing memory transactions significantly boosts performance, especially for large-scale models.
Mixed precision training, another hardware-aware optimization, reduces resource usage by combining lower-precision data types like FP16 (16-bit floating point) with higher-precision types (FP32) for critical calculations. This approach trades a minimal loss in precision for a substantial gain in processing speed and memory efficiency, enabling larger batch sizes and faster processing. Rust’s support for mixed precision is achieved through libraries that interface with CUDA and other acceleration libraries. During mixed precision training, calculations that don’t require high precision, like forward and backward propagation, are computed in FP16, while the final steps, like gradient updates, maintain FP32 precision to prevent numerical instability. The trade-offs in precision are carefully managed to ensure that model accuracy remains high while resource usage and computation times decrease, a critical balance for efficient LLM training.
Rust’s bindings to hardware-specific libraries like CUDA, ROCm, and OneAPI extend its utility for implementing such hardware-accelerated techniques, as these libraries expose low-level functionality that allows fine control over memory allocation, data transfers, and kernel operations. For example, using CUDA with Rust, developers can customize memory management through cuda-sys and cust, providing direct access to device memory, stream control, and kernel launches. This level of control is essential for LLMs, as they require vast memory and efficient data management to support their complex architectures.
Integrating hardware accelerators into Rust-based training pipelines presents challenges related to compatibility and performance tuning. Ensuring compatibility involves configuring Rust to work with various hardware libraries and ensuring that each operation executes with minimal latency. Performance tuning, meanwhile, involves profiling and adjusting kernel execution, data transfer rates, and memory usage, which are critical for maintaining throughput and reducing idle times on the GPU or TPU. By optimizing each step in the training pipeline, Rust-based systems can leverage the maximum potential of accelerators, ensuring that the training process remains efficient and scalable.
Mixed precision training and model parallelism are two significant advancements in deep learning that address the challenges of large models and computational efficiency. As neural networks grow in complexity, they demand more memory and computational power, often exceeding the capabilities of a single device or standard precision calculations. Mixed precision training leverages FP16 (half-precision) operations for forward passes and FP32 (single-precision) for backward passes. This approach optimizes memory usage, speeds up computations, and minimizes power consumption. By performing the forward pass in FP16, memory and computational requirements are reduced, allowing for faster training without significant loss in accuracy. The backward pass, which calculates gradients, remains in FP32 to maintain numerical stability in weight updates, which is crucial for converging to optimal solutions.
Model parallelism is another technique essential for managing large models that do not fit entirely on one device. Instead of using only data parallelism (where the dataset is split across devices), model parallelism splits the model's layers or components, enabling different devices or threads to process parts of the model simultaneously. This approach enhances efficiency and ensures that models can be trained even when they exceed single-device memory limits. By combining model parallelism with mixed precision training, we can achieve faster training for large models while managing hardware resources effectively.
use ndarray::{Array, Array2, Axis, s};
use ndarray_rand::rand_distr::Uniform;
use ndarray_rand::RandomExt;
use std::sync::{Arc, Mutex};
use std::thread;
use std::time::Instant;
use cust::memory::DeviceBuffer;
use cust::{CudaContext, CudaFlags};
// Define hyperparameters
const INPUT_SIZE: usize = 10;
const HIDDEN_SIZE: usize = 64;
const OUTPUT_SIZE: usize = 1;
const LEARNING_RATE: f32 = 0.01;
const BATCH_SIZE: usize = 64;
const EPOCHS: usize = 10;
struct NeuralNetwork {
w1: Arc<Mutex<DeviceBuffer<f16>>>,
b1: Arc<Mutex<DeviceBuffer<f16>>>,
w2: Arc<Mutex<DeviceBuffer<f16>>>,
b2: Arc<Mutex<DeviceBuffer<f16>>>,
}
impl NeuralNetwork {
fn new(context: &CudaContext) -> Self {
let w1 = DeviceBuffer::from_slice(
&Array::random((INPUT_SIZE, HIDDEN_SIZE), Uniform::new(-0.5, 0.5))
.mapv(|x| x as f16)
.into_raw_vec(),
)
.unwrap();
let b1 = DeviceBuffer::from_slice(
&Array::zeros((1, HIDDEN_SIZE)).mapv(|x| x as f16).into_raw_vec(),
)
.unwrap();
let w2 = DeviceBuffer::from_slice(
&Array::random((HIDDEN_SIZE, OUTPUT_SIZE), Uniform::new(-0.5, 0.5))
.mapv(|x| x as f16)
.into_raw_vec(),
)
.unwrap();
let b2 = DeviceBuffer::from_slice(
&Array::zeros((1, OUTPUT_SIZE)).mapv(|x| x as f16).into_raw_vec(),
)
.unwrap();
NeuralNetwork {
w1: Arc::new(Mutex::new(w1)),
b1: Arc::new(Mutex::new(b1)),
w2: Arc::new(Mutex::new(w2)),
b2: Arc::new(Mutex::new(b2)),
}
}
fn forward_layer1(&self, x: &Array2<f32>, context: &CudaContext) -> DeviceBuffer<f16> {
let w1 = self.w1.lock().unwrap();
let b1 = self.b1.lock().unwrap();
// Perform dot product and activation (FP16 precision)
// Implement CUDA kernel or use cuBLAS for matrix multiplication in FP16
// Placeholder - replace with actual CUDA operation
let h1 = x.dot(&*w1).mapv(f32::tanh).mapv(|v| v as f16);
DeviceBuffer::from_slice(&h1.into_raw_vec()).unwrap()
}
fn forward_layer2(&self, h1: &DeviceBuffer<f16>, context: &CudaContext) -> DeviceBuffer<f16> {
let w2 = self.w2.lock().unwrap();
let b2 = self.b2.lock().unwrap();
// Perform dot product (FP16 precision) and return FP16 output
// Placeholder - replace with actual CUDA operation
DeviceBuffer::from_slice(&[0.0f16; OUTPUT_SIZE]).unwrap() // Adjust with real operations
}
fn backward_layer1(&self, d_w1: Array2<f32>, d_b1: Array2<f32>) {
let mut w1 = self.w1.lock().unwrap();
let mut b1 = self.b1.lock().unwrap();
// Update weights (FP32 precision)
*w1 -= &(d_w1 * LEARNING_RATE) as f16;
*b1 -= &(d_b1 * LEARNING_RATE) as f16;
}
fn backward_layer2(&self, d_w2: Array2<f32>, d_b2: Array2<f32>) {
let mut w2 = self.w2.lock().unwrap();
let mut b2 = self.b2.lock().unwrap();
// Update weights (FP32 precision)
*w2 -= &(d_w2 * LEARNING_RATE) as f16;
*b2 -= &(d_b2 * LEARNING_RATE) as f16;
}
}
fn generate_synthetic_data(n: usize) -> (Array2<f32>, Array2<f32>) {
let x = Array::random((n, INPUT_SIZE), Uniform::new(0., 1.));
let y = x.sum_axis(Axis(1)).to_shape((n, OUTPUT_SIZE)).unwrap().to_owned();
(x, y)
}
fn train_model_parallel(nn: Arc<NeuralNetwork>, x: &Array2<f32>, y: &Array2<f32>, context: &CudaContext) {
let h1 = nn.forward_layer1(x, context);
let output = nn.forward_layer2(&h1, context);
// Calculate gradients in FP32 for stability
// Placeholder for CUDA kernel calls
let error = &output - y;
let d_w2 = h1.t().dot(&error).to_owned();
let d_b2 = error.sum_axis(Axis(0)).to_shape((1, OUTPUT_SIZE)).unwrap().to_owned();
let nn1 = nn.clone();
let nn2 = nn.clone();
let x_clone = x.clone();
let backward1_handle = thread::spawn(move || {
let d_hidden = error.dot(&nn2.w2.lock().unwrap().t()) * (1. - h1.mapv(|v| v.powi(2)));
let d_w1 = x_clone.t().dot(&d_hidden).to_owned();
let d_b1 = d_hidden.sum_axis(Axis(0)).to_shape((1, HIDDEN_SIZE)).unwrap().to_owned();
nn2.backward_layer1(d_w1, d_b1);
});
nn1.backward_layer2(d_w2, d_b2);
backward1_handle.join().unwrap();
}
fn main() {
let context = CudaContext::new(CudaFlags::SCHED_AUTO).unwrap();
let (x, y) = generate_synthetic_data(1000);
let nn = Arc::new(NeuralNetwork::new(&context));
let start = Instant::now();
for epoch in 0..EPOCHS {
for i in (0..x.len_of(Axis(0))).step_by(BATCH_SIZE) {
let end_idx = std::cmp::min(i + BATCH_SIZE, x.len_of(Axis(0)));
let x_batch = x.slice(s![i..end_idx, ..]).to_owned();
let y_batch = y.slice(s![i..end_idx, ..]).to_owned();
train_model_parallel(nn.clone(), &x_batch, &y_batch, &context);
}
println!("Epoch {} completed.", epoch + 1);
}
println!("Training completed in {:?}", start.elapsed());
}
The provided code demonstrates a basic neural network setup in Rust with mixed precision and model parallelism capabilities. The network weights and biases are stored as FP16 values on the GPU, utilizing cust (CUDA for Rust) and cuda-sys for GPU-based computations. In the forward_layer1 and forward_layer2 functions, forward passes are conducted in FP16, leveraging the speed and memory efficiency of half-precision operations. For the backward pass, gradients are computed in FP32 to maintain stability. The code distributes gradient calculations across threads, with each thread processing a component of the model independently. The train_model_parallel function handles this by launching separate threads to perform partial updates on different layers. After each epoch, it logs progress, tracking training time and epochs for performance assessment. Overall, this code exemplifies how mixed precision and model parallelism can be combined to accelerate training of neural networks using Rust and GPU resources.
Experimenting with hardware-specific optimizations, like kernel fusion and memory management, improves the performance of Rust-based training pipelines on GPUs. Kernel fusion, implemented in Rust through CUDA, reduces the number of memory transactions, minimizing latency. Memory management optimizations, like pre-allocating memory and caching data on the GPU, reduce I/O bottlenecks, allowing the model to process batches continuously without waiting for data transfers. Profiling tools in Rust can identify performance bottlenecks, such as idle GPU cores or inefficient memory access patterns, and guide adjustments in memory allocation or kernel configurations to achieve smoother training.
Benchmarking Rust-based training pipelines on different hardware setups allows for comparisons in training speed, accuracy, and resource utilization. For example, training on an NVIDIA A100 GPU versus a V100 GPU can reveal the impact of improved hardware support for mixed precision and memory bandwidth on training efficiency. Benchmarks also provide insights into which optimizations yield the most significant performance gains, such as the speed increase from mixed precision training on newer hardware or the latency reduction from kernel fusion on multi-GPU setups.
Hardware-accelerated training techniques have significant applications across various industries. In healthcare, accelerated model training enables faster development of predictive models for diagnostics, processing large datasets of medical records and images in real-time. In autonomous vehicles, hardware-optimized LLMs improve response times for systems processing complex sensor data streams, crucial for real-time decision-making. Trends in hardware acceleration focus on custom chip development, such as Google’s TPU and Amazon’s Trainium, which are optimized for AI workloads. These advancements, combined with Rust’s hardware control capabilities, make it a powerful language for implementing high-performance, hardware-aware AI systems.
In conclusion, hardware acceleration and optimization are pivotal for scaling LLM training effectively, and Rust’s robust support for CUDA, ROCm, and low-level memory management makes it an ideal environment for these tasks. By applying techniques like kernel fusion, mixed precision training, and customized memory management, Rust-based training pipelines can achieve substantial improvements in speed and resource efficiency. These optimizations not only enhance performance on GPUs and TPUs but also contribute to the broader adoption of Rust in machine learning, positioning it as a competitive choice for developing scalable, efficient AI systems.
12.5. Optimization Algorithms for Efficient Training
Optimization algorithms are essential for training large language models (LLMs), providing the techniques needed to iteratively adjust model parameters, minimize loss, and ultimately improve model accuracy. Popular optimization algorithms for LLMs include Stochastic Gradient Descent (SGD), Adam, RMSprop, and LAMB. Each of these algorithms offers unique benefits in convergence speed, stability, and resource efficiency:
Stochastic Gradient Descent (SGD): This classic algorithm updates model weights based on mini-batches, which are small subsets of the full dataset. By doing so, SGD can perform faster updates and make the training process less computationally intensive compared to full-batch updates. However, SGD may converge slowly, especially on complex, high-dimensional problems like LLMs.
Adam (Adaptive Moment Estimation): Adam is a popular choice for training LLMs because it combines momentum and adaptive learning rates. Momentum helps smooth the optimization path by giving preference to previous gradients, while adaptive learning rates allow different parameters to have unique adjustment rates. This combination enables Adam to handle diverse data distributions effectively, making it robust for LLMs.
RMSprop: This algorithm adjusts learning rates based on recent gradient magnitudes. By adapting step sizes according to the variance of gradients, RMSprop is especially useful in models where gradient scales vary across different layers.
LAMB (Layer-wise Adaptive Moments for Batch Training): LAMB is designed for training large-batch models by scaling learning rates in proportion to layer norms, which helps maintain stability across layers. This makes it highly effective for training very large models, such as LLMs.
Efficient training requires minimizing the number of steps to reach acceptable accuracy levels, which is achieved through techniques like learning rate schedules, warm restarts, and adaptive learning rates:
Learning Rate Schedules: These adjust the learning rate over time, often using decay formulas like exponential decay. For instance, an exponential decay function $\eta_t = \eta_0 \times e^{-\lambda t}$ reduces the learning rate as training progresses, allowing for larger steps initially and finer adjustments near convergence. This approach helps models stabilize as they approach an optimal solution.
Warm Restarts: This technique periodically resets the learning rate, allowing the model to escape local minima and explore different regions of the solution space. By periodically increasing the learning rate, warm restarts can lead to improved convergence and better final accuracy.
Rust’s strong type safety and precise control over numeric types provide an ideal environment for implementing these techniques. Rust allows stable updates as parameters dynamically adjust, ensuring safety in matrix operations and minimizing runtime errors. In Rust, implementing optimization algorithms and convergence techniques involves leveraging crates like tch-rs and candle. Both libraries support efficient tensor operations and custom optimization routines, and they offer GPU acceleration when available. The tch-rs crate uses PyTorch's backend, making it highly compatible with pre-trained PyTorch models. The candle crate, on the other hand, provides a more Rust-centric approach, offering greater flexibility for implementing custom optimizers from scratch.
This code demonstrates the implementation of a simple feedforward neural network with two layers using the Rust programming language. The network is trained using synthetic data generated to match a basic regression task, where the model learns to approximate the sum of input features. To optimize the model’s weights, the Adam optimizer is applied, which combines momentum and adaptive learning rates to enhance convergence and stability during training. Rust’s ndarray library is used for handling matrix operations, and the neural network parameters are managed using Arc and Mutex to support concurrent access in multi-threaded environments. The model undergoes several epochs of training, and batch processing is used to improve efficiency by iteratively updating the model with small subsets of data.
use ndarray::{Array, Array2, Axis, s};
use ndarray_rand::rand_distr::Uniform;
use ndarray_rand::RandomExt;
use std::sync::{Arc, Mutex};
use std::time::Instant;
// Define hyperparameters
const INPUT_SIZE: usize = 10;
const HIDDEN_SIZE: usize = 64;
const OUTPUT_SIZE: usize = 1;
const LEARNING_RATE: f32 = 0.01;
const BATCH_SIZE: usize = 64;
const EPOCHS: usize = 10;
// Adam optimizer struct
struct Adam {
learning_rate: f32,
beta1: f32,
beta2: f32,
epsilon: f32,
t: usize,
m_w1: Array2<f32>,
v_w1: Array2<f32>,
m_b1: Array2<f32>,
v_b1: Array2<f32>,
m_w2: Array2<f32>,
v_w2: Array2<f32>,
m_b2: Array2<f32>,
v_b2: Array2<f32>,
}
impl Adam {
fn new(shape_w1: (usize, usize), shape_b1: (usize, usize), shape_w2: (usize, usize), shape_b2: (usize, usize), learning_rate: f32) -> Self {
Self {
learning_rate,
beta1: 0.9,
beta2: 0.999,
epsilon: 1e-8,
t: 0,
m_w1: Array2::zeros(shape_w1),
v_w1: Array2::zeros(shape_w1),
m_b1: Array2::zeros(shape_b1),
v_b1: Array2::zeros(shape_b1),
m_w2: Array2::zeros(shape_w2),
v_w2: Array2::zeros(shape_w2),
m_b2: Array2::zeros(shape_b2),
v_b2: Array2::zeros(shape_b2),
}
}
fn update_w2(&mut self, param: &mut Array2<f32>, grad: &Array2<f32>) {
self.t += 1;
self.m_w2 = self.beta1 * &self.m_w2 + (1.0 - self.beta1) * grad;
self.v_w2 = self.beta2 * &self.v_w2 + (1.0 - self.beta2) * grad.mapv(|x| x * x);
let m_hat = &self.m_w2 / (1.0 - self.beta1.powi(self.t as i32));
let v_hat = &self.v_w2 / (1.0 - self.beta2.powi(self.t as i32));
*param -= &(self.learning_rate * &m_hat / (v_hat.mapv(f32::sqrt) + self.epsilon));
}
fn update_b2(&mut self, param: &mut Array2<f32>, grad: &Array2<f32>) {
self.m_b2 = self.beta1 * &self.m_b2 + (1.0 - self.beta1) * grad;
self.v_b2 = self.beta2 * &self.v_b2 + (1.0 - self.beta2) * grad.mapv(|x| x * x);
let m_hat = &self.m_b2 / (1.0 - self.beta1.powi(self.t as i32));
let v_hat = &self.v_b2 / (1.0 - self.beta2.powi(self.t as i32));
*param -= &(self.learning_rate * &m_hat / (v_hat.mapv(f32::sqrt) + self.epsilon));
}
fn update_w1(&mut self, param: &mut Array2<f32>, grad: &Array2<f32>) {
self.m_w1 = self.beta1 * &self.m_w1 + (1.0 - self.beta1) * grad;
self.v_w1 = self.beta2 * &self.v_w1 + (1.0 - self.beta2) * grad.mapv(|x| x * x);
let m_hat = &self.m_w1 / (1.0 - self.beta1.powi(self.t as i32));
let v_hat = &self.v_w1 / (1.0 - self.beta2.powi(self.t as i32));
*param -= &(self.learning_rate * &m_hat / (v_hat.mapv(f32::sqrt) + self.epsilon));
}
fn update_b1(&mut self, param: &mut Array2<f32>, grad: &Array2<f32>) {
self.m_b1 = self.beta1 * &self.m_b1 + (1.0 - self.beta1) * grad;
self.v_b1 = self.beta2 * &self.v_b1 + (1.0 - self.beta2) * grad.mapv(|x| x * x);
let m_hat = &self.m_b1 / (1.0 - self.beta1.powi(self.t as i32));
let v_hat = &self.v_b1 / (1.0 - self.beta2.powi(self.t as i32));
*param -= &(self.learning_rate * &m_hat / (v_hat.mapv(f32::sqrt) + self.epsilon));
}
}
// Define neural network structure
struct NeuralNetwork {
w1: Arc<Mutex<Array2<f32>>>,
b1: Arc<Mutex<Array2<f32>>>,
w2: Arc<Mutex<Array2<f32>>>,
b2: Arc<Mutex<Array2<f32>>>,
}
impl NeuralNetwork {
fn new() -> Self {
let w1 = Array::random((INPUT_SIZE, HIDDEN_SIZE), Uniform::new(-0.5, 0.5));
let b1 = Array::zeros((1, HIDDEN_SIZE));
let w2 = Array::random((HIDDEN_SIZE, OUTPUT_SIZE), Uniform::new(-0.5, 0.5));
let b2 = Array::zeros((1, OUTPUT_SIZE));
NeuralNetwork {
w1: Arc::new(Mutex::new(w1)),
b1: Arc::new(Mutex::new(b1)),
w2: Arc::new(Mutex::new(w2)),
b2: Arc::new(Mutex::new(b2)),
}
}
fn forward_layer1(&self, x: &Array2<f32>) -> Array2<f32> {
let w1 = self.w1.lock().unwrap();
let b1 = self.b1.lock().unwrap();
(x.dot(&*w1) + &*b1).mapv(f32::tanh)
}
fn forward_layer2(&self, h1: &Array2<f32>) -> Array2<f32> {
let w2 = self.w2.lock().unwrap();
let b2 = self.b2.lock().unwrap();
h1.dot(&*w2) + &*b2
}
}
// Generate synthetic data
fn generate_synthetic_data(n: usize) -> (Array2<f32>, Array2<f32>) {
let x = Array::random((n, INPUT_SIZE), Uniform::new(0., 1.));
let y = x.sum_axis(Axis(1)).to_shape((n, OUTPUT_SIZE)).unwrap().to_owned();
(x, y)
}
// Train the model
fn train_model(nn: Arc<NeuralNetwork>, x: &Array2<f32>, y: &Array2<f32>, optimizer: &mut Adam) {
let h1 = nn.forward_layer1(x);
let output = nn.forward_layer2(&h1);
let error = &output - y;
let d_w2 = h1.t().dot(&error).to_owned();
let d_b2 = error.sum_axis(Axis(0)).to_shape((1, OUTPUT_SIZE)).unwrap().to_owned();
// Update layer 2 weights
{
let mut nn_w2 = nn.w2.lock().unwrap();
optimizer.update_w2(&mut nn_w2, &d_w2);
}
{
let mut nn_b2 = nn.b2.lock().unwrap();
optimizer.update_b2(&mut nn_b2, &d_b2);
}
// Calculate gradients for layer 1
let nn_w2 = nn.w2.lock().unwrap();
let d_hidden = error.dot(&nn_w2.t()).mapv(|x| 1. - x.powi(2));
let d_w1 = x.t().dot(&d_hidden).to_owned();
let d_b1 = d_hidden.sum_axis(Axis(0)).to_shape((1, HIDDEN_SIZE)).unwrap().to_owned();
// Update layer 1 weights
{
let mut nn_w1 = nn.w1.lock().unwrap();
optimizer.update_w1(&mut nn_w1, &d_w1);
}
{
let mut nn_b1 = nn.b1.lock().unwrap();
optimizer.update_b1(&mut nn_b1, &d_b1);
}
}
fn main() {
let (x, y) = generate_synthetic_data(1000);
let nn = Arc::new(NeuralNetwork::new());
let mut optimizer = Adam::new((INPUT_SIZE, HIDDEN_SIZE), (1, HIDDEN_SIZE), (HIDDEN_SIZE, OUTPUT_SIZE), (1, OUTPUT_SIZE), LEARNING_RATE);
let start = Instant::now();
for epoch in 0..EPOCHS {
for i in (0..x.len_of(Axis(0))).step_by(BATCH_SIZE) {
let end_idx = std::cmp::min(i + BATCH_SIZE, x.len_of(Axis(0)));
let x_batch = x.slice(s![i..end_idx, ..]).to_owned();
let y_batch = y.slice(s![i..end_idx, ..]).to_owned();
train_model(nn.clone(), &x_batch, &y_batch, &mut optimizer);
}
println!("Epoch {} completed", epoch + 1);
}
println!("Training completed in {:?}", start.elapsed());
}
The code defines separate update functions for each layer’s weights and biases within the Adam optimizer, resolving issues with Rust’s strict borrowing rules. Each epoch performs mini-batch training, updating the network’s parameters based on calculated gradients, which are stored and managed independently for each layer. After each forward pass, the gradients are computed for both layers, and the Adam optimizer updates the parameters using these gradients, along with stored moving averages. The code exemplifies the use of memory-safe concurrency in Rust while handling potentially complex data transformations, enabling efficient and safe updates across multiple threads. This approach highlights Rust’s concurrency capabilities for machine learning tasks, allowing for safe parameter updates without mutable borrow conflicts.
The candle crate provides a Rust-native interface to define custom optimization routines. In this scenario, we’re building a text generation pipeline using Rust with the candle library, incorporating a custom optimizer to update model parameters based on gradients. The goal is to generate text sequences given a prompt by applying a machine learning model (such as a transformer-based language model) and using an optimizer with an exponential decay learning rate. This setup is useful for fine-tuning models, allowing control over parameter adjustments to enhance text generation quality, and provides a scalable approach for model deployment and updates.
[dependencies]
anyhow = "1.0"
serde_json = "1.0.132"
reqwest = { version = "0.12.8", features = ["blocking"] }
candle-transformers = "0.7.2"
candle-core = "0.7.2"
candle-nn = "0.7.2"
hf-hub = "0.3.2"
tokenizers = "0.19"
candle-examples = "0.7.2"
tracing-subscriber = "0.3.18"
tracing-chrome = "0.7.2"
use anyhow::{Error as E, Result};
use candle_core::{DType, Device, Tensor, utils, Var};
use candle_nn::VarBuilder;
use candle_transformers::models::based::Model;
use candle_transformers::generation::LogitsProcessor;
use candle_examples::token_output_stream::TokenOutputStream;
use hf_hub::{api::sync::Api, Repo, RepoType};
use tokenizers::Tokenizer;
use std::time::Instant;
use std::io::Write;
struct TextGeneration {
model: Model,
device: Device,
tokenizer: TokenOutputStream,
logits_processor: LogitsProcessor,
repeat_penalty: f32,
repeat_last_n: usize,
optimizer: CustomOptimizer,
}
impl TextGeneration {
#[allow(clippy::too_many_arguments)]
fn new(
model: Model,
tokenizer: Tokenizer,
seed: u64,
temp: Option<f64>,
top_p: Option<f64>,
repeat_penalty: f32,
repeat_last_n: usize,
device: &Device,
learning_rate: f64,
decay_rate: f64,
) -> Self {
let logits_processor = LogitsProcessor::new(seed, temp, top_p);
let optimizer = CustomOptimizer::new(learning_rate, decay_rate);
Self {
model,
tokenizer: TokenOutputStream::new(tokenizer),
logits_processor,
repeat_penalty,
repeat_last_n,
device: device.clone(),
optimizer,
}
}
fn run(&mut self, prompt: &str, sample_len: usize) -> Result<()> {
self.tokenizer.clear();
let mut tokens = self
.tokenizer
.tokenizer()
.encode(prompt, true)
.map_err(E::msg)?
.get_ids()
.to_vec();
for &t in tokens.iter() {
if let Some(t) = self.tokenizer.next_token(t)? {
print!("{t}");
}
}
std::io::stdout().flush()?;
let mut generated_tokens = 0usize;
let eos_token = match self.tokenizer.get_token("<|endoftext|>") {
Some(token) => token,
None => anyhow::bail!("cannot find the <|endoftext|> token"),
};
let start_gen = Instant::now();
for index in 0..sample_len {
let context_size = if index > 0 { 1 } else { tokens.len() };
let start_pos = tokens.len().saturating_sub(context_size);
let ctxt = &tokens[start_pos..];
let input = Tensor::new(ctxt, &self.device)?.unsqueeze(0)?;
let logits = self.model.forward(&input, start_pos)?;
let logits = logits.squeeze(0)?.squeeze(0)?.to_dtype(DType::F32)?;
let logits = if self.repeat_penalty == 1. {
logits
} else {
let start_at = tokens.len().saturating_sub(self.repeat_last_n);
candle_transformers::utils::apply_repeat_penalty(
&logits,
self.repeat_penalty,
&tokens[start_at..],
)?
};
let next_token = self.logits_processor.sample(&logits)?;
tokens.push(next_token);
generated_tokens += 1;
if next_token == eos_token {
break;
}
if let Some(t) = self.tokenizer.next_token(next_token)? {
print!("{t}");
std::io::stdout().flush()?;
}
}
let dt = start_gen.elapsed();
if let Some(rest) = self.tokenizer.decode_rest().map_err(E::msg)? {
print!("{rest}");
}
std::io::stdout().flush()?;
println!(
"\n{generated_tokens} tokens generated ({:.2} token/s)",
generated_tokens as f64 / dt.as_secs_f64(),
);
Ok(())
}
// Example method to apply optimizer for parameter update
fn update_parameters(&mut self, gradients: &[Tensor]) -> Result<()> {
// Placeholder: Replace `&mut []` with actual model parameters if accessible
self.optimizer.apply_gradients(&mut [], gradients)
}
}
struct CustomOptimizer {
learning_rate: f64,
decay_rate: f64,
step: usize,
}
impl CustomOptimizer {
fn new(learning_rate: f64, decay_rate: f64) -> Self {
Self {
learning_rate,
decay_rate,
step: 0,
}
}
fn apply_gradients(&mut self, vars: &mut [Var], gradients: &[Tensor]) -> Result<()> {
let current_lr = self.learning_rate * (self.decay_rate.powf(self.step as f64));
self.step += 1;
for (var, grad) in vars.iter_mut().zip(gradients) {
// Scale the gradient by the current learning rate.
let update = (grad * current_lr)?;
// Compute the new value by subtracting the update from the original tensor.
let updated_tensor = var.as_tensor().sub(&update)?;
// Reassign the variable to the updated tensor using `from_tensor`.
*var = Var::from_tensor(&updated_tensor)?;
}
Ok(())
}
}
fn main() -> Result<()> {
let tracing_enabled = true; // Enable or disable tracing.
let prompt = "Once upon a time"; // The prompt text for generation.
let temperature = Some(0.7); // Sampling temperature.
let top_p = Some(0.9); // Nucleus sampling probability cutoff.
let seed = 299792458; // Random seed for generation.
let sample_len = 100; // Number of tokens to generate.
let model_id = "hazyresearch/based-360m".to_string(); // Model ID to use.
let revision = "refs/pr/1".to_string(); // Model revision.
let repeat_penalty = 1.1; // Repeat penalty factor.
let repeat_last_n = 64; // Context size for repeat penalty.
let cpu = true; // Whether to use CPU or GPU.
use tracing_chrome::ChromeLayerBuilder;
use tracing_subscriber::prelude::*;
let _guard = if tracing_enabled {
let (chrome_layer, guard) = ChromeLayerBuilder::new().build();
tracing_subscriber::registry().with(chrome_layer).init();
Some(guard)
} else {
None
};
println!(
"avx: {}, neon: {}, simd128: {}, f16c: {}",
utils::with_avx(),
utils::with_neon(),
utils::with_simd128(),
utils::with_f16c()
);
let start = Instant::now();
let api = Api::new()?;
let repo = api.repo(Repo::with_revision(
model_id,
RepoType::Model,
revision,
));
let config_file = repo.get("config.json")?;
let filenames = vec![repo.get("model.safetensors")?];
let repo = api.model("openai-community/gpt2".to_string());
let tokenizer_file = repo.get("tokenizer.json")?;
println!("retrieved the files in {:?}", start.elapsed());
let tokenizer = Tokenizer::from_file(tokenizer_file).map_err(E::msg)?;
let start = Instant::now();
let config = serde_json::from_reader(std::fs::File::open(config_file)?)?;
let device = candle_examples::device(cpu)?;
let dtype = if device.is_cuda() {
DType::BF16
} else {
DType::F32
};
let vb = unsafe { VarBuilder::from_mmaped_safetensors(&filenames, dtype, &device)? };
let model = Model::new(&config, vb)?;
println!("loaded the model in {:?}", start.elapsed());
let mut pipeline = TextGeneration::new(
model,
tokenizer,
seed,
temperature,
top_p,
repeat_penalty,
repeat_last_n,
&device,
0.01, // Initial learning rate for optimizer
0.99, // Decay rate for learning rate
);
pipeline.run(&prompt, sample_len)?;
// Assuming you have computed gradients, apply optimizer update
let gradients = vec![]; // Placeholder for actual gradient tensors
pipeline.update_parameters(&gradients)?;
Ok(())
}
The code initializes a text generation system with a TextGeneration struct that holds the model, tokenizer, and a custom optimizer (CustomOptimizer). The optimizer applies gradient-based updates with an exponential decay learning rate to fine-tune model parameters. The run function in TextGeneration generates text based on a given prompt by encoding it into tokens, passing them through the model, and sampling generated tokens until reaching the desired sequence length. The custom optimizer (CustomOptimizer) manages parameter updates, and each gradient update is scaled by a decaying learning rate. The main function orchestrates model and device setup, retrieves model files, initializes the pipeline, and triggers text generation, demonstrating a full setup for text generation and fine-tuning in Rust.
Optimization algorithms impact training efficiency, particularly in balancing convergence speed with model stability. For instance, while SGD offers simplicity and low computational overhead, it often requires additional techniques like momentum or adaptive learning rates to achieve stable convergence in complex LLMs. Regularization techniques, such as L2 regularization and dropout, are crucial in maintaining efficient training by preventing overfitting. L2 regularization, defined as $\frac{\lambda}{2} \sum \theta^2$, penalizes large weights, promoting smoother model parameters and reducing the risk of overfitting. Dropout randomly deactivates neurons during training, which helps generalize the model by exposing it to varied representations. Rust’s type safety and memory management allow for efficient implementation of these regularization methods, enhancing model robustness without overextending computational resources.
Advanced optimization techniques, including gradient clipping and weight decay, further improve training outcomes by controlling parameter updates. Gradient clipping prevents exploding gradients by capping the gradient magnitude at a predefined threshold ccc, ensuring that parameter updates remain within a manageable range. This technique is especially important in recurrent architectures or deep networks, where gradients can grow excessively large. Weight decay, similar to L2 regularization, applies a constant decay rate to weights, preventing excessive growth and promoting model stability. Rust’s precision control ensures accurate implementation of these techniques, providing a stable foundation for efficient and effective training.
Experimenting with various learning rate schedules and adaptive learning rates in Rust can reveal optimal configurations for fast and stable convergence. For example, cosine annealing adjusts the learning rate according to a cosine function, allowing smooth transitions between high and low rates, defined as:
$$ \eta_t = \eta_{\text{min}} + \frac{1}{2}(\eta_{\text{max}} - \eta_{\text{min}}) \left(1 + \cos\left(\frac{t}{T}\pi\right)\right) $$
Such schedules maintain rapid progress during initial training stages and gradually slow updates as the model approaches convergence. Rust’s efficient handling of trigonometric functions and type-safe arithmetic ensures precise implementation of such schedules, maximizing the benefits of adaptive training rates without risking numerical instability.
Analyzing the trade-offs between optimization techniques involves evaluating training speed, model accuracy, and resource utilization. Optimization algorithms like LAMB (Layer-wise Adaptive Moments for Batch training) are tailored for large batch training, maintaining high throughput while balancing convergence stability. LAMB, which scales gradients based on layer-wise normalization, is ideal for distributed training setups, as it allows for large batches without compromising stability. For smaller batch sizes, Adam or RMSprop may offer faster convergence due to their adaptability in handling noisy gradients. In real-world applications, these trade-offs impact decisions on algorithm selection, as faster convergence with minimal resource use is essential in cost-sensitive industries like finance or e-commerce.
Layer-wise Adaptive Moments for Batch training (LAMB) is an advanced optimization algorithm designed to improve training efficiency for large-scale neural networks, particularly in the context of very large batch sizes. LAMB is especially useful for training LLM architectures where batch sizes exceed the limits of traditional optimizers like SGD or Adam. The essence of LAMB is its ability to balance layer-wise learning rates by applying adaptive moment estimates and scaling each layer independently. This approach helps prevent layers with larger gradients from dominating updates and stabilizes training, even with massive models that require high computational resources. This stability makes LAMB a popular choice in distributed training, where large batch sizes leverage multiple GPUs or nodes effectively, improving convergence rates and enabling efficient scaling.
LAMB incorporates two main mechanisms: adaptive moments and layer-wise learning rate scaling. Similar to optimizers like Adam, LAMB maintains exponential moving averages of gradients and squared gradients (first and second moments) to adaptively tune each parameter. However, in addition to this, it computes the weight norm and gradient norm for each layer separately. These norms are used to scale the update for each layer individually, balancing the update magnitudes across layers. Additionally, LAMB includes optional weight decay, which applies regularization without affecting the adaptive moment calculations, a feature particularly useful in large, over-parameterized models.
[dependencies]
anyhow = "1.0"
ndarray = "0.16.1"
ndarray-rand = "0.15.0"
use ndarray::{Array2, Axis, Zip};
use ndarray_rand::RandomExt;
use ndarray_rand::rand_distr::Normal;
use std::collections::HashMap;
// Hyperparameters
const LEARNING_RATE: f32 = 0.001;
const BETA1: f32 = 0.9;
const BETA2: f32 = 0.999;
const EPSILON: f32 = 1e-6;
const WEIGHT_DECAY_RATE: f32 = 0.01;
// Define the LAMB optimizer
struct Lamb {
lr: f32,
beta1: f32,
beta2: f32,
epsilon: f32,
weight_decay_rate: f32,
m: HashMap<String, Array2<f32>>, // First moment
v: HashMap<String, Array2<f32>>, // Second moment
}
impl Lamb {
fn new(lr: f32, beta1: f32, beta2: f32, epsilon: f32, weight_decay_rate: f32) -> Self {
Self {
lr,
beta1,
beta2,
epsilon,
weight_decay_rate,
m: HashMap::new(),
v: HashMap::new(),
}
}
fn initialize_params(&mut self, params: &HashMap<String, Array2<f32>>) {
for (name, param) in params {
self.m.insert(name.clone(), Array2::zeros(param.raw_dim()));
self.v.insert(name.clone(), Array2::zeros(param.raw_dim()));
}
}
fn step(&mut self, params: &mut HashMap<String, Array2<f32>>, grads: &HashMap<String, Array2<f32>>, step: i32) {
let beta1_t = self.beta1.powi(step);
let beta2_t = self.beta2.powi(step);
for (name, param) in params.iter_mut() {
if let Some(grad) = grads.get(name) {
let m = self.m.get_mut(name).unwrap();
let v = self.v.get_mut(name).unwrap();
// Reborrow `m` and `v` to avoid moving them
Zip::from(&mut *m).and(grad).for_each(|m, &g| *m = self.beta1 * *m + (1.0 - self.beta1) * g);
Zip::from(&mut *v).and(grad).for_each(|v, &g| *v = self.beta2 * *v + (1.0 - self.beta2) * g * g);
// Bias-corrected first and second moment
let m_hat = m.mapv(|mi| mi / (1.0 - beta1_t));
let v_hat = v.mapv(|vi| vi / (1.0 - beta2_t));
// Weight decay term
let weight_decay_adjustment = param.mapv(|p| p * self.weight_decay_rate);
let mut update = &m_hat / (v_hat.mapv(f32::sqrt) + self.epsilon);
if self.should_apply_weight_decay(name) {
update = &update + &weight_decay_adjustment;
}
// Layer adaptation ratio
let ratio = if self.should_apply_layer_adaptation(name) {
let w_norm = param.mapv(|x| x.powi(2)).sum().sqrt();
let g_norm = update.mapv(|x| x.powi(2)).sum().sqrt();
if w_norm > 0.0 && g_norm > 0.0 {
w_norm / g_norm
} else {
1.0
}
} else {
1.0
};
// Apply update
Zip::from(param).and(&update).for_each(|p, &u| *p -= ratio * self.lr * u);
}
}
}
fn should_apply_weight_decay(&self, param_name: &str) -> bool {
// Custom logic to exclude parameters from weight decay, if necessary
!param_name.contains("bias")
}
fn should_apply_layer_adaptation(&self, param_name: &str) -> bool {
// Custom logic to exclude parameters from layer adaptation, if necessary
!param_name.contains("layer_norm")
}
}
// Simple neural network model for demonstration
struct SimpleNet {
params: HashMap<String, Array2<f32>>,
}
impl SimpleNet {
fn new(input_dim: usize, hidden_dim: usize, output_dim: usize) -> Self {
let w1 = Array2::random((input_dim, hidden_dim), Normal::new(0.0, 0.1).unwrap());
let b1 = Array2::zeros((1, hidden_dim));
let w2 = Array2::random((hidden_dim, output_dim), Normal::new(0.0, 0.1).unwrap());
let b2 = Array2::zeros((1, output_dim));
let mut params = HashMap::new();
params.insert("w1".to_string(), w1);
params.insert("b1".to_string(), b1);
params.insert("w2".to_string(), w2);
params.insert("b2".to_string(), b2);
SimpleNet { params }
}
fn forward(&self, x: &Array2<f32>) -> Array2<f32> {
let hidden = x.dot(&self.params["w1"]) + &self.params["b1"];
let hidden = hidden.mapv(|x| x.max(0.0)); // ReLU
hidden.dot(&self.params["w2"]) + &self.params["b2"]
}
fn compute_gradients(&self, x: &Array2<f32>, target: &Array2<f32>, pred: &Array2<f32>) -> HashMap<String, Array2<f32>> {
let mut grads = HashMap::new();
let grad_output = 2.0 * (pred - target) / target.len() as f32;
let grad_w2 = self.params["w1"].t().dot(&grad_output);
let grad_b2 = grad_output.sum_axis(Axis(0)).insert_axis(Axis(0));
let grad_hidden = grad_output.dot(&self.params["w2"].t());
let grad_hidden_relu = grad_hidden.mapv(|x| if x > 0.0 { x } else { 0.0 });
let grad_w1 = x.t().dot(&grad_hidden_relu);
let grad_b1 = grad_hidden_relu.sum_axis(Axis(0)).insert_axis(Axis(0));
grads.insert("w1".to_string(), grad_w1);
grads.insert("b1".to_string(), grad_b1);
grads.insert("w2".to_string(), grad_w2);
grads.insert("b2".to_string(), grad_b2);
grads
}
}
fn main() {
let input_dim = 128;
let hidden_dim = 64;
let output_dim = 10;
let mut model = SimpleNet::new(input_dim, hidden_dim, output_dim);
let mut optimizer = Lamb::new(LEARNING_RATE, BETA1, BETA2, EPSILON, WEIGHT_DECAY_RATE);
optimizer.initialize_params(&model.params);
for epoch in 1..=100 {
let x = Array2::random((128, input_dim), Normal::new(0.0, 1.0).unwrap());
let target = Array2::random((128, output_dim), Normal::new(0.0, 1.0).unwrap());
let pred = model.forward(&x);
let grads = model.compute_gradients(&x, &target, &pred);
optimizer.step(&mut model.params, &grads, epoch);
let loss = (pred - &target).mapv(|x| x.powi(2)).mean().unwrap();
println!("Epoch: {}, Loss: {:.4}", epoch, loss);
}
}
In the provided Rust code, we define a LAMB optimizer from scratch using the ndarray crate for matrix and tensor operations. The Lamb struct initializes and maintains moving averages (m and v) for each parameter, which are updated during each optimization step. The step function iterates over each parameter and corresponding gradient to compute the first and second moments, applies bias correction, and calculates the layer-wise scaling factor for updates. A simple neural network model (SimpleNet) demonstrates how to use the optimizer: for each training epoch, the network computes predictions, calculates the loss, computes gradients, and then updates the parameters using LAMB. This setup effectively showcases the layer-wise adaptation and scaling properties of the LAMB optimizer.
The provided Rust code introduces a Layer-wise Adaptive Moments (LAMB) optimizer implemented with tch, a crate that provides Rust bindings to the PyTorch library. This implementation encapsulates LAMB's core principles within the Lamb struct, which manages the first and second moments (m and v) for each parameter, using tensors from the tch crate to handle tensor operations natively on GPU or CPU. This code achieves a similar goal to the earlier scratch implementation in ndarray, but now it leverages the higher-level tensor operations provided by tch. Specifically, it allows for more seamless integration with neural networks and parameter management within tch’s ecosystem, as seen in the SimpleNet struct. This SimpleNet model defines a simple neural network, demonstrates LAMB’s usage through parameter initialization, and performs forward and gradient computation efficiently using tch's functions for tensor manipulation, like mm (matrix multiplication) and relu.
[dependencies]
anyhow = "1.0"
ndarray = "0.16.1"
ndarray-rand = "0.15.0"
tch = "0.12.0"
use std::collections::HashMap;
use tch::{nn, Device, Kind, Tensor};
// Hyperparameters
const LEARNING_RATE: f64 = 0.001;
const BETA1: f64 = 0.9;
const BETA2: f64 = 0.999;
const EPSILON: f64 = 1e-6;
const WEIGHT_DECAY_RATE: f64 = 0.01;
// Define the LAMB optimizer
struct Lamb {
lr: f64,
beta1: f64,
beta2: f64,
epsilon: f64,
weight_decay_rate: f64,
m: HashMap<String, Tensor>, // First moment
v: HashMap<String, Tensor>, // Second moment
}
impl Lamb {
fn new(lr: f64, beta1: f64, beta2: f64, epsilon: f64, weight_decay_rate: f64) -> Self {
Self {
lr,
beta1,
beta2,
epsilon,
weight_decay_rate,
m: HashMap::new(),
v: HashMap::new(),
}
}
fn initialize_params(&mut self, params: &HashMap<String, Tensor>) {
for (name, param) in params {
self.m.insert(name.clone(), Tensor::zeros_like(param));
self.v.insert(name.clone(), Tensor::zeros_like(param));
}
}
fn step(&mut self, params: &mut HashMap<String, Tensor>, grads: &HashMap<String, Tensor>, step: i32) {
let beta1_t = self.beta1.powi(step);
let beta2_t = self.beta2.powi(step);
for (name, param) in params.iter_mut() {
if let Some(grad) = grads.get(name) {
let m = self.m.get_mut(name).unwrap();
let v = self.v.get_mut(name).unwrap();
// Update moments with gradients
*m = &*m * self.beta1 + (1.0 - self.beta1) * grad;
*v = &*v * self.beta2 + (1.0 - self.beta2) * grad.square();
// Bias-corrected moments
let m_hat = &*m / (1.0 - beta1_t);
let v_hat = &*v / (1.0 - beta2_t);
// Weight decay term
let weight_decay_adjustment = &*param * self.weight_decay_rate;
let mut update = &m_hat / (v_hat.sqrt() + self.epsilon);
if self.should_apply_weight_decay(name) {
update += &weight_decay_adjustment;
}
// Layer adaptation ratio
let ratio = if self.should_apply_layer_adaptation(name) {
let w_norm = param.norm();
let g_norm = update.norm();
if w_norm.double_value(&[]) > 0.0 && g_norm.double_value(&[]) > 0.0 {
w_norm / g_norm
} else {
Tensor::from(1.0)
}
} else {
Tensor::from(1.0)
};
// Apply the update
*param = &*param - &(ratio * self.lr * update);
}
}
}
fn should_apply_weight_decay(&self, param_name: &str) -> bool {
// Exclude weight decay for specific parameter names if necessary
!param_name.contains("bias")
}
fn should_apply_layer_adaptation(&self, param_name: &str) -> bool {
// Exclude layer adaptation for specific parameter names if necessary
!param_name.contains("layer_norm")
}
}
// Simple neural network model for demonstration
struct SimpleNet {
params: HashMap<String, Tensor>,
}
impl SimpleNet {
fn new(vs: &nn::Path, input_dim: i64, hidden_dim: i64, output_dim: i64) -> Self {
let w1 = vs.randn("w1", &[input_dim, hidden_dim], 0.0, 0.1);
let b1 = vs.zeros("b1", &[hidden_dim]);
let w2 = vs.randn("w2", &[hidden_dim, output_dim], 0.0, 0.1);
let b2 = vs.zeros("b2", &[output_dim]);
let mut params = HashMap::new();
params.insert("w1".to_string(), w1);
params.insert("b1".to_string(), b1);
params.insert("w2".to_string(), w2);
params.insert("b2".to_string(), b2);
SimpleNet { params }
}
fn forward(&self, x: &Tensor) -> Tensor {
let hidden = x.mm(&self.params["w1"]) + &self.params["b1"];
let hidden = hidden.relu(); // ReLU activation
hidden.mm(&self.params["w2"]) + &self.params["b2"]
}
fn compute_gradients(&self, x: &Tensor, target: &Tensor, pred: &Tensor) -> HashMap<String, Tensor> {
let mut grads = HashMap::new();
let grad_output = 2.0 * (pred - target) / target.size()[0] as f64;
let grad_w2 = self.params["w1"].transpose(-1, -2).mm(&grad_output);
let grad_b2 = grad_output.sum_dim_intlist(&[0i64][..], false, Kind::Float);
let grad_hidden = grad_output.mm(&self.params["w2"].transpose(-1, -2));
let grad_hidden_relu = grad_hidden * (self.params["b1"].relu()).sign();
let grad_w1 = x.transpose(-1, -2).mm(&grad_hidden_relu);
let grad_b1 = grad_hidden_relu.sum_dim_intlist(&[0i64][..], false, Kind::Float);
grads.insert("w1".to_string(), grad_w1);
grads.insert("b1".to_string(), grad_b1);
grads.insert("w2".to_string(), grad_w2);
grads.insert("b2".to_string(), grad_b2);
grads
}
}
fn main() {
let vs = nn::VarStore::new(Device::cuda_if_available());
let input_dim = 128;
let hidden_dim = 64;
let output_dim = 10;
let mut model = SimpleNet::new(&vs.root(), input_dim, hidden_dim, output_dim);
let mut optimizer = Lamb::new(LEARNING_RATE, BETA1, BETA2, EPSILON, WEIGHT_DECAY_RATE);
optimizer.initialize_params(&model.params);
for epoch in 1..=100 {
let x = Tensor::randn(&[128, input_dim], (Kind::Float, Device::cuda_if_available()));
let target = Tensor::randn(&[128, output_dim], (Kind::Float, Device::cuda_if_available()));
let pred = model.forward(&x);
let grads = model.compute_gradients(&x, &target, &pred);
optimizer.step(&mut model.params, &grads, epoch);
let loss = (pred - &target).pow_tensor_scalar(2).mean(Kind::Float);
println!("Epoch: {}, Loss: {:.4}", epoch, loss.double_value(&[]));
}
}
In comparison to the scratch implementation using ndarray, this version is more concise and integrates directly with the tch library’s support for GPU operations, optimized tensor handling, and automatic differentiation features, making it more suitable for complex deep learning workflows. Instead of manually iterating and computing gradients with ndarray operations, tch’s methods like transpose, sum_dim_intlist, and mm handle these operations efficiently. This version also includes parameter management directly within tch, using VarStore to initialize and store model parameters, which simplifies handling during training and eliminates the need for lower-level tensor initialization and computation found in ndarray. This makes it especially suitable for high-performance deep learning tasks.
Industry applications of optimization algorithms in Rust-based training pipelines span fields such as natural language processing, healthcare, and automated customer service, where rapid training convergence is essential. In customer service chatbots, for instance, efficient optimization algorithms allow models to be retrained frequently, adapting to new user queries and enhancing response accuracy. Healthcare applications benefit from rapid convergence in medical imaging analysis, where adaptive learning rates help models quickly adapt to complex and heterogeneous datasets. Emerging trends in optimization, such as hybrid optimizers and dynamic learning rates, further enhance Rust’s role in high-performance LLM training by combining the stability of traditional optimizers with the speed of adaptive techniques.
In conclusion, optimization algorithms are integral to efficient LLM training, and Rust’s capabilities in memory management, type safety, and low-level performance make it ideal for implementing advanced optimization techniques. By balancing convergence speed, model accuracy, and resource efficiency, Rust-based optimization algorithms can streamline LLM training, offering scalable, high-performance solutions for industry applications. These optimizations are foundational in advancing LLM technology, ensuring that models remain accurate, adaptable, and resource-efficient in complex training environments.
12.6. Profiling and Monitoring Training Performance
Profiling and monitoring are essential components of efficient training, enabling developers to identify bottlenecks and optimize training pipelines. By systematically observing metrics such as memory usage, CPU and GPU utilization, and I/O performance, profiling helps uncover inefficiencies in resource allocation and code execution. Profiling also reveals how different components of a training pipeline interact, highlighting areas where optimization can yield significant performance improvements. Rust’s performance-centric ecosystem, coupled with tools such as perf, cargo-flamegraph, and specialized GPU profilers, provides the means to implement detailed profiling setups, allowing developers to make data-driven optimizations that minimize training time and maximize resource efficiency.
Memory profiling is particularly important in large language model (LLM) training, where high memory demands can slow down or even halt training if resources are exhausted. Profiling memory usage in Rust involves tracking allocations and deallocations across the model, ensuring that data is managed efficiently without memory leaks. Tools like cargo-flamegraph provide a visual representation of function calls and memory usage, making it easier to pinpoint high-memory consumption points. Mathematically, the memory demand $M_{total}$ of a model can be expressed as the sum of individual layer requirements $M_i$:
$$M_{total} = \sum_{i=1}^n M_i$$
where $n$ represents the number of layers. Analyzing this memory distribution enables developers to optimize allocations, such as by pre-allocating memory for recurrent tensors, reducing dynamic memory usage, and improving overall stability.
CPU and GPU utilization profiling offers insights into computational resource usage, which is critical in balancing load across processors. Efficient CPU and GPU utilization ensures that each processor is actively contributing to computations without unnecessary idle time. In Rust, tools such as perf allow developers to track CPU utilization, while GPU profiling tools like cuda-memcheck provide data on GPU memory usage and processing efficiency. Profiling results can reveal issues such as CPU-GPU communication delays or suboptimal GPU kernel launches, which are often areas ripe for optimization. For instance, if GPU utilization is low, data transfer times between CPU and GPU could be optimized by overlapping data preparation with GPU computation, effectively reducing idle time and maximizing parallelism.
Figure 4: Optimization strategy for LLM training.
Real-time monitoring complements profiling by providing continuous updates on training progress, alerting developers to emerging issues before they become critical. Setting up real-time monitoring involves logging metrics like loss, accuracy, and latency, allowing developers to track trends and respond to deviations quickly. Logging frameworks in Rust, such as log and env_logger, support structured logging for efficient metric tracking, while dashboards such as Grafana can visualize these logs, offering a comprehensive view of training performance. Real-time monitoring is particularly useful in distributed training setups, where synchronization errors or data inconsistencies can cause model divergence if not detected early. Automated alerts provide another layer of protection, notifying developers of threshold breaches in key metrics such as memory usage or loss spikes, ensuring that interventions are timely.
Key metrics to monitor during training include training loss, validation accuracy, resource utilization, and batch processing time. Each metric offers a unique insight into the training pipeline's performance. For example, a sudden increase in batch processing time might indicate an I/O bottleneck or memory swap, while unexpected changes in training loss could signal gradient explosion or model instability. Understanding these metrics’ relationships helps developers diagnose issues effectively. For instance, memory usage and GPU utilization are often correlated; high memory usage with low GPU utilization may point to inefficient data transfer or caching. By establishing metric baselines, deviations become more apparent, enabling faster identification of root causes.
Profiling distributed and parallel training setups presents additional challenges due to the complexity of inter-node communication and data synchronization. Profiling such setups requires distributed tracing to track data flow and identify latency points across nodes. Rust’s concurrency features, like async/await, aid in profiling by isolating asynchronous operations, allowing developers to pinpoint areas where distributed nodes may be waiting for synchronization. Network profiling tools, such as Wireshark, complement Rust’s built-in tracing by monitoring data packets, revealing communication delays that could impede training speed.
Automated dashboards and alerting systems play a crucial role in maintaining efficient training pipelines, especially in cloud-based or distributed setups where constant human monitoring is impractical. By automating alerts for threshold violations in metrics like GPU temperature, memory usage, and loss plateauing, developers can be instantly notified of performance issues. Alerts allow for quick diagnosis, whether for a memory leak, underutilized GPU, or unstable loss function, and prompt developers to apply appropriate optimizations. Dashboards like Prometheus and Grafana support automated data scraping and visualization, providing an integrated solution for monitoring Rust-based LLM training pipelines.
Profiling and monitoring are fundamental for optimizing large language model (LLM) training pipelines, where efficiency is crucial due to high memory and computational demands. Rust’s ecosystem, known for its performance and low-level control, provides a solid foundation for implementing a detailed profiling setup. Profiling involves tracking metrics such as memory usage, CPU and GPU utilization, and I/O performance to pinpoint bottlenecks and optimize resource allocation. Memory profiling, for instance, is essential in LLM training, where each layer contributes to the model’s total memory demand. By using profiling tools like cargo-flamegraph for Rust, developers can visualize memory and CPU consumption, making it easier to identify functions consuming high resources. This approach aids in optimizing memory allocation strategies, such as pre-allocating recurrent tensors and minimizing dynamic memory usage, thereby improving model stability and reducing training times.
CPU and GPU utilization profiling is equally important to ensure balanced load distribution across processors. Tools like perf can track CPU usage, while GPU profilers, such as cuda-memcheck, provide data on GPU memory usage and kernel efficiency. These profiling tools help diagnose issues like CPU-GPU communication delays or underutilized GPU resources, allowing developers to optimize data transfer times or adjust the kernel configurations. For instance, by overlapping CPU data preparation with GPU computation, idle times can be minimized, enhancing parallelism. Real-time monitoring complements profiling by providing continuous feedback on metrics like training loss, accuracy, and batch processing time. Rust’s log crate, in conjunction with monitoring dashboards like Grafana, enables structured logging of these metrics, providing insights into the training pipeline's health and alerting developers to performance deviations.
This Rust code demonstrates a custom implementation of the LAMB (Layer-wise Adaptive Moments) optimizer applied to train a simple neural network, using the tch crate for tensor operations and model management. The code initializes a neural network model (SimpleNet) with two layers, where each layer’s parameters (weights and biases) are stored in a HashMap for easy access and updating. The optimizer (Lamb) manages the first and second moments for each parameter, which it updates during each training step, along with bias correction and layer-wise adaptation. The env_logger and log crates are used to add logging functionality that tracks and displays key metrics, including the loss value and duration for each epoch, to monitor training progress.
[dependencies]
anyhow = "1.0"
env_logger = "0.11.5"
log = "0.4.22"
ndarray = "0.16.1"
ndarray-rand = "0.15.0"
tch = "0.12.0"
use std::collections::HashMap;
use std::time::Instant;
use log::{info, LevelFilter};
use env_logger;
use tch::{nn, Device, Kind, Tensor};
// Hyperparameters
const LEARNING_RATE: f64 = 0.001;
const BETA1: f64 = 0.9;
const BETA2: f64 = 0.999;
const EPSILON: f64 = 1e-6;
const WEIGHT_DECAY_RATE: f64 = 0.01;
// Define the LAMB optimizer
struct Lamb {
lr: f64,
beta1: f64,
beta2: f64,
epsilon: f64,
weight_decay_rate: f64,
m: HashMap<String, Tensor>, // First moment
v: HashMap<String, Tensor>, // Second moment
}
impl Lamb {
fn new(lr: f64, beta1: f64, beta2: f64, epsilon: f64, weight_decay_rate: f64) -> Self {
Self {
lr,
beta1,
beta2,
epsilon,
weight_decay_rate,
m: HashMap::new(),
v: HashMap::new(),
}
}
fn initialize_params(&mut self, params: &HashMap<String, Tensor>) {
for (name, param) in params {
self.m.insert(name.clone(), Tensor::zeros_like(param));
self.v.insert(name.clone(), Tensor::zeros_like(param));
}
}
fn step(&mut self, params: &mut HashMap<String, Tensor>, grads: &HashMap<String, Tensor>, step: i32) {
let beta1_t = self.beta1.powi(step);
let beta2_t = self.beta2.powi(step);
for (name, param) in params.iter_mut() {
if let Some(grad) = grads.get(name) {
let m = self.m.get_mut(name).unwrap();
let v = self.v.get_mut(name).unwrap();
// Update moments with gradients
*m = &*m * self.beta1 + (1.0 - self.beta1) * grad;
*v = &*v * self.beta2 + (1.0 - self.beta2) * grad.square();
// Bias-corrected moments
let m_hat = &*m / (1.0 - beta1_t);
let v_hat = &*v / (1.0 - beta2_t);
// Weight decay term
let weight_decay_adjustment = &*param * self.weight_decay_rate;
let mut update = &m_hat / (v_hat.sqrt() + self.epsilon);
if self.should_apply_weight_decay(name) {
update += &weight_decay_adjustment;
}
// Layer adaptation ratio
let ratio = if self.should_apply_layer_adaptation(name) {
let w_norm = param.norm();
let g_norm = update.norm();
if w_norm.double_value(&[]) > 0.0 && g_norm.double_value(&[]) > 0.0 {
w_norm / g_norm
} else {
Tensor::from(1.0)
}
} else {
Tensor::from(1.0)
};
// Apply the update
*param = &*param - &(ratio * self.lr * update);
}
}
}
fn should_apply_weight_decay(&self, param_name: &str) -> bool {
// Exclude weight decay for specific parameter names if necessary
!param_name.contains("bias")
}
fn should_apply_layer_adaptation(&self, param_name: &str) -> bool {
// Exclude layer adaptation for specific parameter names if necessary
!param_name.contains("layer_norm")
}
}
// Simple neural network model for demonstration
struct SimpleNet {
params: HashMap<String, Tensor>,
}
impl SimpleNet {
fn new(vs: &nn::Path, input_dim: i64, hidden_dim: i64, output_dim: i64) -> Self {
let w1 = vs.randn("w1", &[input_dim, hidden_dim], 0.0, 0.1);
let b1 = vs.zeros("b1", &[hidden_dim]);
let w2 = vs.randn("w2", &[hidden_dim, output_dim], 0.0, 0.1);
let b2 = vs.zeros("b2", &[output_dim]);
let mut params = HashMap::new();
params.insert("w1".to_string(), w1);
params.insert("b1".to_string(), b1);
params.insert("w2".to_string(), w2);
params.insert("b2".to_string(), b2);
SimpleNet { params }
}
fn forward(&self, x: &Tensor) -> Tensor {
let hidden = x.mm(&self.params["w1"]) + &self.params["b1"];
let hidden = hidden.relu(); // ReLU activation
hidden.mm(&self.params["w2"]) + &self.params["b2"]
}
fn compute_gradients(&self, x: &Tensor, target: &Tensor, pred: &Tensor) -> HashMap<String, Tensor> {
let mut grads = HashMap::new();
let grad_output = 2.0 * (pred - target) / target.size()[0] as f64;
let grad_w2 = self.params["w1"].transpose(-1, -2).mm(&grad_output);
let grad_b2 = grad_output.sum_dim_intlist(&[0i64][..], false, Kind::Float);
let grad_hidden = grad_output.mm(&self.params["w2"].transpose(-1, -2));
let grad_hidden_relu = grad_hidden * (self.params["b1"].relu()).sign();
let grad_w1 = x.transpose(-1, -2).mm(&grad_hidden_relu);
let grad_b1 = grad_hidden_relu.sum_dim_intlist(&[0i64][..], false, Kind::Float);
grads.insert("w1".to_string(), grad_w1);
grads.insert("b1".to_string(), grad_b1);
grads.insert("w2".to_string(), grad_w2);
grads.insert("b2".to_string(), grad_b2);
grads
}
}
fn main() {
// Initialize the logger
env_logger::Builder::new()
.filter_level(LevelFilter::Info)
.init();
let vs = nn::VarStore::new(Device::cuda_if_available());
let input_dim = 128;
let hidden_dim = 64;
let output_dim = 10;
let mut model = SimpleNet::new(&vs.root(), input_dim, hidden_dim, output_dim);
let mut optimizer = Lamb::new(LEARNING_RATE, BETA1, BETA2, EPSILON, WEIGHT_DECAY_RATE);
optimizer.initialize_params(&model.params);
for epoch in 1..=100 {
let start_time = Instant::now();
let x = Tensor::randn(&[128, input_dim], (Kind::Float, Device::cuda_if_available()));
let target = Tensor::randn(&[128, output_dim], (Kind::Float, Device::cuda_if_available()));
let pred = model.forward(&x);
let grads = model.compute_gradients(&x, &target, &pred);
optimizer.step(&mut model.params, &grads, epoch);
let loss = (pred - &target).pow_tensor_scalar(2).mean(Kind::Float);
let epoch_duration = start_time.elapsed();
// Log the loss and duration
info!("Epoch: {}, Loss: {:.4}, Duration: {:?}", epoch, loss.double_value(&[]), epoch_duration);
}
}
The code works by iterating over a set number of epochs to train the network on randomly generated data. Each epoch starts by recording the time, computing the model's predictions, and calculating gradients using backpropagation to update the parameters. The LAMB optimizer's step function then updates each parameter by calculating its adjusted learning rate based on the parameter's layer-wise scaling and decay. After each epoch, the logger outputs the epoch number, loss value, and epoch duration, enabling real-time tracking of the network’s training performance and helping identify any potential bottlenecks in computation. This approach can be extended to include more advanced profiling or monitoring methods to further analyze training efficiency.
Different optimization strategies can be tested based on profiling results to improve training efficiency. For instance, if memory profiling reveals high consumption due to repeated tensor allocations, pre-allocating memory for tensors can reduce reallocations and improve memory usage. Similarly, if profiling shows that data loading times are contributing to bottlenecks, parallelizing data loading with Rust’s rayon crate can improve batch processing speed. Experimenting with these strategies based on real-time profiling results provides actionable insights for optimizing the training pipeline effectively.
Profiling and monitoring are essential in industries relying on AI for real-time applications, such as autonomous vehicles and healthcare, where latency and stability are crucial. In autonomous driving, continuous monitoring of training pipelines allows for fast model updates based on recent sensor data, while profiling ensures that resources are allocated efficiently to maintain low-latency processing. In healthcare, where models analyze complex patient data, profiling and monitoring ensure that models are trained accurately and efficiently without excessive memory or computation demands. Emerging trends in profiling and monitoring emphasize the use of distributed tracing and automated performance alerts, making Rust’s concurrency and real-time logging support valuable for achieving robust training pipelines.
In conclusion, profiling and monitoring are indispensable for maintaining and optimizing training pipelines, and Rust’s performance-oriented features provide an ideal environment for these tasks. By using detailed profiling, real-time monitoring, and automated alerts, Rust-based systems can achieve high-efficiency training, identify and address bottlenecks, and maintain stable model performance. This integrated approach to profiling and monitoring enables developers to scale LLMs effectively, ensuring optimal resource utilization and timely issue resolution in complex training environments.
12.7. Case Studies and Applications
The exploration of efficient training techniques using Rust has enabled breakthroughs in deploying large language models (LLMs) across various sectors, such as healthcare, finance, and manufacturing. This section dives into case studies demonstrating the practical application of these techniques, revealing how Rust’s performance-oriented capabilities and ecosystem uniquely address challenges like scalability, resource management, and optimization in LLM training. Each case highlights how advanced Rust features, such as precise memory control, concurrency, and the ability to interface with hardware acceleration, can be leveraged to meet the demands of real-world projects. Through these studies, readers can gain insights into the transformative potential of Rust-based training practices, as well as the future trajectory for efficient LLM deployment in data-intensive fields.
In healthcare, a notable case involved training diagnostic models on patient datasets, which are both large and sensitive. Given the high dimensionality of this data, the project adopted data parallelism and mixed precision techniques in Rust. Data parallelism allowed patient records to be distributed across nodes, improving computational efficiency, while mixed precision training reduced memory usage by mixing FP16 and FP32 operations. This approach not only enhanced training speed but also conserved memory resources, facilitating larger batch sizes without sacrificing model accuracy. Mixed precision, a technique that maintains performance with reduced memory by performing certain calculations in FP16, was critical in meeting stringent latency and privacy requirements, highlighting Rust’s capacity to handle complex datasets with high efficiency and precision.
In the financial industry, another case study showcased the deployment of a real-time recommendation model for stock analysis, a task requiring continuous data ingestion and adaptation to fast-changing market conditions. Rust’s low-level control over memory and parallel processing enabled the construction of a high-throughput data pipeline. Kernel fusion—a technique that combines several operations into a single GPU kernel to minimize data transfer overhead—along with memory pre-allocation, significantly enhanced GPU utilization. By fusing operations, the team achieved a 40% reduction in data transfer time, enabling faster updates and more accurate recommendations. This setup underscores Rust’s strengths in dynamic environments, where rapid data processing is vital, such as in finance, where timely predictions are integral to strategic decision-making.
These case studies reveal several key takeaways on optimization and scaling. One of the foremost insights is the critical importance of efficient memory and resource utilization when training LLMs with large, continuously updated datasets, such as those in finance. The healthcare case illustrates how memory management and hardware acceleration can be used effectively for high-dimensional, privacy-sensitive data. These findings underscore that selecting the right optimization techniques—such as data parallelism or kernel fusion—depends on the specific requirements of each domain, and Rust’s adaptability in handling both high-performance computations and precise memory control offers an edge for LLM training.
Furthermore, these examples emphasize the broader impact of efficient training on LLM scalability and adaptability. Real-time data applications in healthcare, finance, and e-commerce are clear beneficiaries, with faster training enabling prompt diagnostic results or real-time market recommendations. The adaptability afforded by techniques like layer-wise scaling and precision control also allows LLMs to be tailored to diverse applications with unique constraints. Rust’s ability to handle such customizations efficiently positions it as a valuable tool for enhancing LLM scalability, particularly for applications needing continuous adaptation to new data.
An essential element in these projects has been the collaborative strength of the Rust community and open-source resources. Libraries like rayon for parallel processing and cuda-sys for GPU interfacing were pivotal in advancing these applications. Open-source contributions have allowed development teams to leverage existing solutions, focusing their efforts on domain-specific fine-tuning rather than fundamental infrastructure. This community-driven ecosystem accelerates progress in efficient training techniques, allowing for widespread sharing of optimizations and best practices that benefit projects of all sizes.
Future applications of these methods could extend to fields like manufacturing, where real-time monitoring and quality control are paramount. For instance, a Rust-based real-time monitoring system for quality assurance could leverage data parallelism to process sensor data from multiple factory nodes and use kernel fusion to optimize GPU utilization, supporting rapid detection and prediction of product defects. By continuously improving resource management and response times, such systems could dramatically improve production efficiency and reduce waste.
In summary, these case studies illustrate how Rust’s robust performance and fine-grained control mechanisms can address the unique demands of LLM training across varied fields. The insights gained from real-world applications underscore Rust’s potential as a foundation for high-performance, scalable machine learning solutions. As the Rust community continues to evolve and expand its toolkit, developers can anticipate even greater advancements in efficient training techniques, empowering future innovations in LLM deployment and other data-intensive domains.
12.8. Conclusion
Chapter 12 equips readers with the knowledge and tools to optimize the training of large language models using Rust. By mastering these efficient training techniques, readers can significantly improve the scalability, speed, and cost-effectiveness of their AI projects, positioning themselves at the forefront of AI development.
12.8.1. Further Learning with GenAI
These prompts cover a wide range of topics, from the basics of setting up an optimized Rust environment to advanced concepts like distributed training, hardware acceleration, and profiling. Each prompt is carefully crafted to encourage deep engagement, pushing readers to explore the nuances and technical challenges involved in optimizing training processes for LLMs in Rust.
Explain the importance of efficient training in the context of large language models. How do resource utilization, time, and cost impact the overall effectiveness of LLM training, and what are the primary challenges involved?
Describe the process of setting up a Rust environment optimized for efficient training of LLMs. What are the key tools and crates required, and how do they contribute to the performance and scalability of training pipelines?
Discuss the differences between parallelism and concurrency in Rust. How can these concepts be leveraged to speed up the training of large models, and what are the challenges in implementing them effectively?
Explore the role of data parallelism and model parallelism in optimizing training for LLMs. What are the advantages and limitations of each approach, and how can they be implemented in Rust using crates like
rayonandtokio?Analyze the challenges of distributed training in scaling up LLM training. How do data synchronization, network communication, and fault tolerance impact the performance of distributed systems, and how can Rust's features help address these challenges?
Discuss the importance of hardware acceleration in training LLMs. How can GPUs, TPUs, and custom accelerators be integrated into Rust-based training pipelines, and what are the key considerations in optimizing their use?
Explain the concept of mixed precision training and its benefits in improving the efficiency of LLM training. How can mixed precision be implemented in Rust, and what impact does it have on training speed and model accuracy?
Explore the role of optimization algorithms like SGD, Adam, and LAMB in efficient training. How do these algorithms influence convergence speed and stability, and how can they be effectively implemented in Rust?
Discuss the significance of learning rate schedules and adaptive learning rates in accelerating convergence. How can these techniques be applied in Rust, and what impact do they have on training efficiency and model performance?
Analyze the trade-offs between different regularization techniques, such as L2 regularization and dropout, in preventing overfitting while maintaining efficient training. How can these techniques be implemented and tuned in Rust?
Explore the challenges of profiling and monitoring training performance in Rust-based pipelines. What tools and techniques can be used to identify bottlenecks, and how can real-time monitoring help optimize training?
Discuss the key metrics to monitor during LLM training. How do memory usage, CPU/GPU utilization, and I/O performance relate to overall training efficiency, and how can these metrics be tracked and analyzed in Rust?
Explain the process of setting up a distributed training pipeline in Rust. What are the key components involved, and how can they be optimized for scalability and efficiency in a cloud-based cluster?
Discuss the role of communication protocols like MPI and gRPC in distributed training. How do these protocols impact the performance of Rust-based training pipelines, and what are the best practices for implementing them?
Analyze the benefits of using Rust’s concurrency model, including async/await and parallel iterators, in optimizing the training of LLMs. How can these features be applied to reduce training time and improve resource utilization?
Explore the challenges of integrating hardware accelerators into Rust-based training pipelines. What are the key considerations in ensuring compatibility and performance, and how can Rust’s ecosystem support these integrations?
Discuss the role of kernel fusion and memory management techniques in optimizing hardware-specific training. How can these techniques be implemented in Rust to improve performance on GPUs and other accelerators?
Explain the process of implementing gradient clipping and weight decay in Rust. How do these techniques contribute to stable and efficient training, particularly in large-scale LLMs?
Analyze the impact of real-time monitoring and logging on maintaining efficient training pipelines. How can automated alerts and dashboards be set up in Rust to detect and address issues early in the training process?
Discuss the broader implications of efficient training techniques for the future of LLM development. How can the techniques explored in this chapter be applied to different domains and applications, and what are the potential challenges and opportunities?
Embrace these challenges with curiosity and determination, knowing that your efforts will not only enhance your technical expertise but also prepare you to contribute to the cutting edge of AI development and innovation.
12.8.2. Hands On Practices
Self-Exercise 12.1: Implementing Data Parallelism in Rust for Efficient Training
Objective: To gain practical experience in implementing data parallelism in Rust, optimizing the training process for large datasets.
Tasks:
Set up a Rust environment and install necessary crates like
rayonfor parallel data processing.Implement a data parallelism strategy for a given LLM training task, splitting the dataset across multiple threads or processes.
Train the model using the parallelized data pipeline, monitoring for any performance bottlenecks or synchronization issues.
Compare the training speed and efficiency of the parallelized approach with a non-parallelized baseline.
Deliverables:
A Rust codebase that implements data parallelism for LLM training.
A performance report comparing the parallelized training process with the baseline, including metrics such as training time, CPU/GPU utilization, and model accuracy.
An analysis of the challenges encountered during implementation and suggestions for further optimization.
Self-Exercise 12.2: Fine-Tuning a Distributed Training Pipeline in Rust
Objective: To develop and fine-tune a distributed training pipeline for large language models using Rust, optimizing for scalability and efficiency.
Tasks:
Implement a distributed training setup in Rust, using communication protocols like MPI or gRPC to coordinate training across multiple nodes.
Fine-tune the distributed pipeline by experimenting with different strategies for data synchronization and load balancing.
Deploy the distributed training pipeline on a cloud-based cluster, monitoring performance under various workloads.
Evaluate the scalability and efficiency of the distributed pipeline, identifying potential bottlenecks and areas for improvement.
Deliverables:
A Rust codebase for a distributed training pipeline, including the implementation of synchronization and communication mechanisms.
A performance evaluation report that includes metrics on scalability, training speed, and resource utilization in a distributed environment.
Recommendations for optimizing distributed training pipelines based on the results of the fine-tuning process.
Self-Exercise 12.3: Profiling and Optimizing Training Performance in Rust
Objective: To profile a Rust-based LLM training pipeline and implement optimizations based on the profiling results to improve efficiency.
Tasks:
Implement a training pipeline in Rust for a large language model, ensuring that the pipeline is instrumented for detailed profiling.
Use profiling tools like
cargo-flamegraphand GPU profilers to identify bottlenecks in the training process, focusing on areas like memory usage, CPU/GPU utilization, and I/O performance.Implement optimizations based on the profiling data, such as memory management improvements, kernel fusion, or adjusting thread concurrency.
Re-profile the optimized training pipeline to evaluate the impact of the changes, and compare the results with the original pipeline.
Deliverables:
A Rust codebase with an optimized training pipeline, including detailed comments on the profiling and optimization process.
A profiling report that highlights the key bottlenecks identified and the strategies used to address them.
A comparative analysis of the training pipeline’s performance before and after optimization, including metrics on training time, resource utilization, and model accuracy.
Self-Exercise 12.4: Implementing Mixed Precision Training in Rust
Objective: To explore the benefits of mixed precision training for large language models by implementing it in Rust and analyzing its impact on training speed and model accuracy.
Tasks:
Implement mixed precision training in Rust using available libraries and crates that support lower-precision arithmetic on GPUs.
Train a large language model using the mixed precision setup, monitoring the impact on both training speed and model convergence.
Compare the results of the mixed precision training with a baseline model trained using standard precision, focusing on metrics such as training time, memory usage, and final model accuracy.
Analyze the trade-offs between precision and performance, identifying scenarios where mixed precision training is most effective.
Deliverables:
A Rust codebase implementing mixed precision training for a large language model.
A performance comparison report that includes metrics on training time, memory usage, and model accuracy for both mixed precision and standard precision training.
An analysis of the effectiveness of mixed precision training, with recommendations for its application in various training scenarios.
Self-Exercise 12.5: Developing a Real-Time Monitoring System for LLM Training in Rust
Objective: To design and implement a real-time monitoring system for tracking the performance of a large language model training pipeline in Rust.
Tasks:
Implement a real-time monitoring framework in Rust, capable of tracking key metrics such as memory usage, CPU/GPU utilization, and training loss.
Integrate the monitoring system with an existing LLM training pipeline, ensuring that data is collected and logged efficiently.
Set up automated alerts and dashboards to provide real-time feedback on training performance, identifying potential issues early in the process.
Test the monitoring system in a live training scenario, analyzing its effectiveness in maintaining efficient training and quickly addressing any performance issues.
Deliverables:
A Rust codebase for a real-time monitoring system integrated with an LLM training pipeline.
A report detailing the implementation of the monitoring system, including the metrics tracked and the alerting mechanisms set up.
An evaluation of the monitoring system’s effectiveness in a live training scenario, with recommendations for further enhancements or adjustments.
Comments