3.1. Introduction to Neural Networks for NLP link

Neural networks have become a fundamental tool for processing and understanding natural language in modern artificial intelligence. At their core, neural networks are built from neurons (also known as units), which are mathematical functions designed to simulate the behavior of biological neurons. Each neuron receives inputs (represented as numerical vectors), applies a weighted transformation, and passes the result through an activation function to determine the output. These neurons are arranged into layers—typically including an input layer, one or more hidden layers, and an output layer—forming what is known as a feedforward neural network (FNN) or Multi Layer Perceptron (MLP) for some historical reason. While FNNs are powerful and have been successfully applied to various machine learning tasks, they face limitations when applied to natural language processing (NLP), primarily because language inherently involves context and sequence, which FNNs are not designed to handle efficiently.

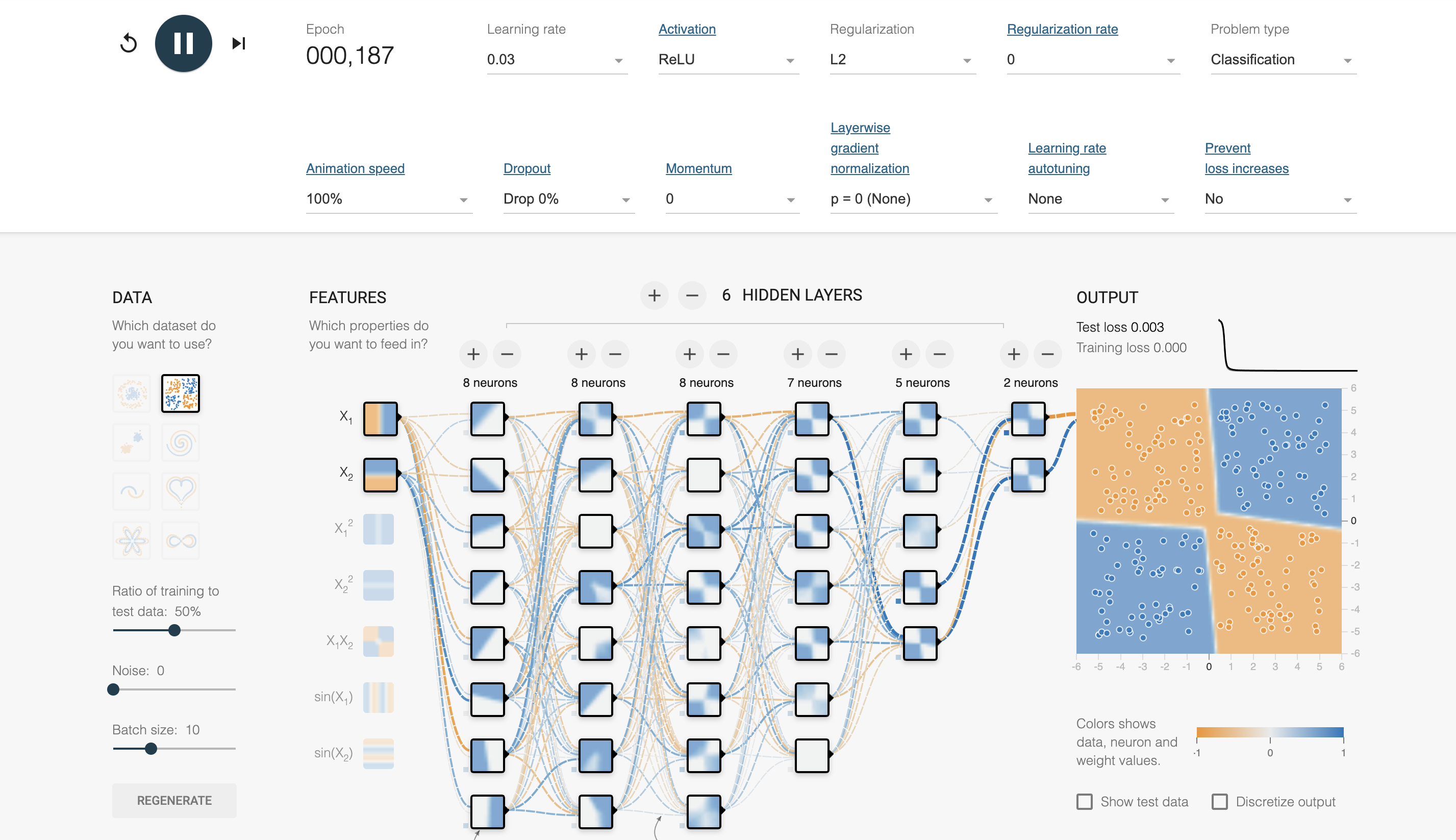
Figure 1: Interactive Learning tool for FNN or MLP architecture (https://deeperplayground.org).

A FNN or MLP is a type of artificial neural network where connections between the nodes do not form a cycle. It consists of multiple layers: an input layer, one or more hidden layers, and an output layer. Each layer is composed of neurons, and each neuron is connected to every neuron in the subsequent layer, allowing for complex transformations of the input data. These models are fundamental in many machine learning tasks, including classification, regression, and pattern recognition.

To explore this architecture using the deeperplayground tool, we begin by generating synthetic 2D data, typically a mixture of simple patterns such as clusters or spirals. The dataset is split into training and testing sets with a predefined ratio, for example, 70% training and 30% testing. The batch size, which controls the number of samples processed before the model updates its parameters, is typically chosen based on the complexity of the data and computational resources.

In this setting, the features of the dataset are two-dimensional, denoted as $x_1$ and $x_2$, representing the coordinates of each point in the 2D space. The goal of the MLP is to learn a decision boundary that separates or classifies the points based on these features. The interaction between $x_1$ and $x_2$ can be linear or involve more complex non-linear relationships, which the network learns during training. Combinations of $x_1$ and $x_2$, such as $x_1^2$, $x_1 x_2$, or $x_2^2$, may be implicitly captured by the model as it learns non-linear transformations through its hidden layers.

The MLP architecture in this scenario consists of two output neurons, corresponding to the two classes of the synthetic data (for binary classification). The hidden layer architecture comprises six hidden layers, each with a maximum of eight neurons. Mathematically, the transformation at each layer $l$ can be represented as:

$$ z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)} $$

$$ a^{(l)} = \sigma(z^{(l)}) $$

Here, $W^{(l)}$ represents the weight matrix of layer $l$, $b^{(l)}$ is the bias vector, $a^{(l-1)}$ is the activation from the previous layer, and $\sigma$ is the activation function applied element-wise (such as ReLU, sigmoid, or tanh). The output layer uses a softmax function for classification, defined as:

$$ \hat{y}_i = \frac{e^{z_i}}{\sum_j e^{z_j}} $$

This ensures that the output probabilities sum to one. The MLP learns by minimizing the cross-entropy loss:

$$ L(y, \hat{y}) = - \sum_i y_i \log(\hat{y}_i) $$

where $y$ is the true label, and $\hat{y}$ is the predicted output.

During the training of a neural network, the process of updating the weights is guided by an optimization algorithm, such as gradient descent, aimed at minimizing the loss function. The loss function, denoted by $L(y, \hat{y})$, quantifies the difference between the true output $y$ and the predicted output $\hat{y}$. The goal is to adjust the model’s parameters (weights and biases) in such a way that the loss function is minimized, thus improving the model's predictive accuracy.

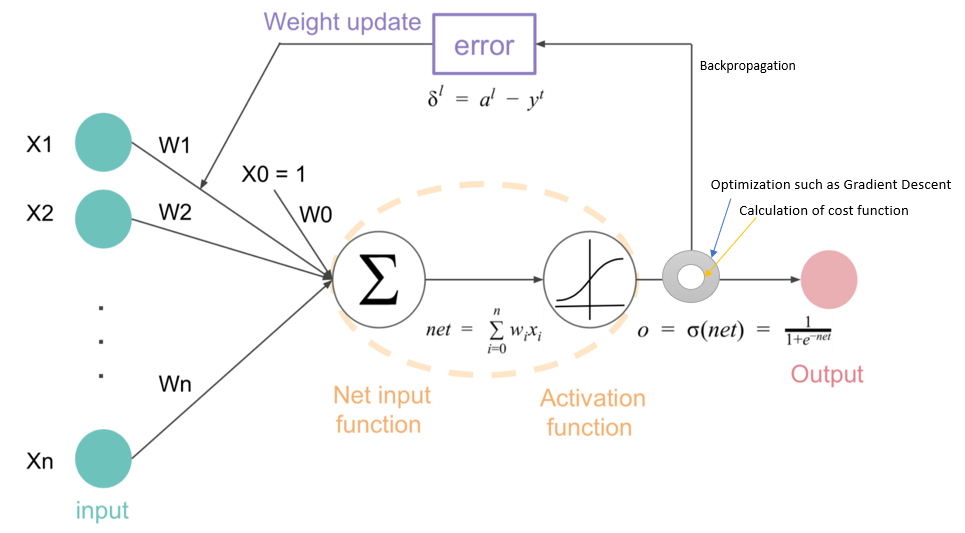
Figure 2: Backpropagation and gradient descent.

To minimize the loss, the gradient descent algorithm computes the gradient of the loss function with respect to each weight $W^{(l)}$ and bias $b^{(l)}$ in the network. This gradient tells us the direction in which the weights should be adjusted to reduce the loss. The weight update rule for a weight $W_{ij}^{(l)}$ in layer $l$, connecting neuron $i$ in layer $l-1$ to neuron $j$ in layer $l$, is defined as:

$$ W_{ij}^{(l)} \leftarrow W_{ij}^{(l)} - \eta \frac{\partial L}{\partial W_{ij}^{(l)}} $$

Here, $\eta$ is the learning rate, a hyperparameter that controls the step size of the update. The term $\frac{\partial L}{\partial W_{ij}^{(l)}}$ is the partial derivative of the loss function with respect to the weight $W_{ij}^{(l)}$, which tells us how much the loss changes with a small change in $W_{ij}^{(l)}$. This derivative is calculated using the backpropagation algorithm, a recursive application of the chain rule of calculus.

For the biases, the update rule is similar:

$$ b_j^{(l)} \leftarrow b_j^{(l)} - \eta \frac{\partial L}{\partial b_j^{(l)}} $$

The backpropagation algorithm works by computing the gradient of the loss function with respect to each weight and bias in the network by propagating the error backwards through the network. For each layer, starting from the output layer, we compute the error at each neuron and propagate this error back to the previous layer. The error signal at layer $l$, denoted by $\delta^{(l)}$, is the gradient of the loss with respect to the weighted input of that layer $z^{(l)}$:

$$ \delta_j^{(l)} = \frac{\partial L}{\partial z_j^{(l)}} $$

This error signal is used to compute the gradients with respect to the weights and biases. For the weights, the gradient is given by:

$$ \frac{\partial L}{\partial W_{ij}^{(l)}} = \delta_j^{(l)} a_i^{(l-1)} $$

where $a_i^{(l-1)}$ is the activation of the iii-th neuron in the previous layer. For the biases, the gradient is simply:

$$ \frac{\partial L}{\partial b_j^{(l)}} = \delta_j^{(l)} $$

The error signal $\delta^{(l)}$ is recursively computed starting from the output layer. For the output layer, it is the derivative of the loss with respect to the weighted input:

$$ \delta_j^{(L)} = \frac{\partial L}{\partial z_j^{(L)}} = \hat{y}_j - y_j $$

For hidden layers, the error is propagated backwards using the derivative of the activation function $\sigma$ and the error from the next layer:

$$ \delta_j^{(l)} = \left( \sum_k W_{jk}^{(l+1)} \delta_k^{(l+1)} \right) \sigma'(z_j^{(l)}) $$

Here, $\sigma'(z_j^{(l)})$ is the derivative of the activation function (e.g., ReLU, sigmoid) applied to the weighted input at neuron $j$ in layer $l$.

Momentum is an extension of gradient descent that helps to accelerate convergence and smooth out the optimization process, especially in the presence of oscillations. It works by adding a fraction of the previous update to the current update, allowing the algorithm to accumulate velocity in directions of consistent gradients. The update rule with momentum is:

$$ v_{ij}^{(l)} \leftarrow \gamma v_{ij}^{(l)} + \eta \frac{\partial L}{\partial W_{ij}^{(l)}} $$

$$ W_{ij}^{(l)} \leftarrow W_{ij}^{(l)} - v_{ij}^{(l)} $$

Here, $v_{ij}^{(l)}$ represents the velocity or momentum term, and $\gamma$ (typically between 0 and 1) is the momentum coefficient. The momentum term accelerates the updates in the relevant direction and dampens oscillations, making it particularly useful in deep networks where gradients may vary significantly across layers.

The learning rate $\eta$ determines the step size for each update. A small learning rate leads to more gradual, but stable, updates, while a large learning rate may cause the optimization to overshoot the minimum of the loss function, potentially causing divergence.

Training is typically done over multiple epochs, where each epoch represents one complete pass through the entire training dataset. The number of epochs is a hyperparameter that affects how long the model trains. Too few epochs may result in underfitting (the model hasn’t learned enough), while too many may lead to overfitting (the model learns noise in the data).

In conclusion, the process of minimizing the loss function in neural networks involves computing gradients via backpropagation, updating the weights and biases through gradient descent, and optionally using momentum to accelerate learning. The learning rate and number of epochs are crucial hyperparameters that govern the speed and convergence of the model's training.

The activation function used in the hidden layers significantly affects the model's ability to capture non-linearities. ReLU is commonly used for hidden layers because it introduces non-linearity while avoiding vanishing gradients. Dropout is applied to prevent overfitting by randomly "dropping" a proportion of neurons during each update, ensuring that the model does not rely too heavily on any particular neuron.

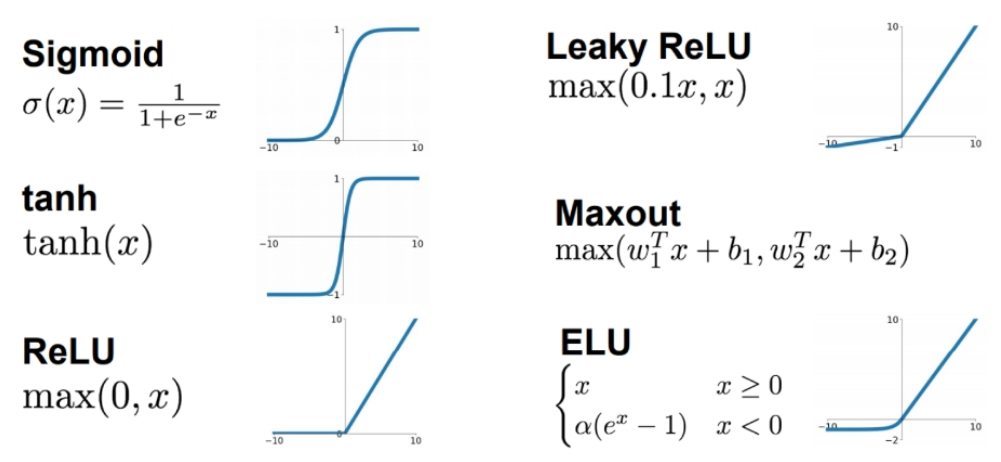
Figure 3: MLP activation functions.

To prevent overfitting and improve generalization, regularization techniques such as $L_2$-regularization (weight decay) are applied, adding a penalty term to the loss function:

$$ L_{\text{reg}} = L(y, \hat{y}) + \lambda \sum_i ||W_i||_2^2 $$

where $\lambda$ is the regularization strength.

Layerwise gradient normalization helps ensure stable learning by normalizing the gradients across different layers, preventing them from becoming too large or too small. This is particularly important in deep networks to prevent gradient vanishing or explosion. Additionally, the learning rate can be auto-tuned during training by using techniques like adaptive learning rates (e.g., AdaGrad or Adam), which dynamically adjust the learning rate based on the gradient's magnitude. Furthermore, mechanisms can be put in place to prevent loss increases, such as early stopping, where training halts if the loss on the validation set begins to rise, or by using gradient clipping to limit the gradient's magnitude, avoiding instability.

In the Deeperplayground tool, the training process can be visualized through real-time plots of the training and testing loss, helping to monitor the model's progress and detect potential overfitting if the training loss decreases while the testing loss rises. The decision boundary evolves as the model learns, and the interplay between the hyperparameters (e.g., learning rate, momentum, regularization) and the model's capacity (number of neurons, layers) becomes apparent as the loss is optimized.

This mathematical framework and visualization through Deeperplayground provides an intuitive yet rigorous understanding of how MLPs work, how they can be tuned, and the impact of their architecture and hyperparameters on the model’s performance.

In NLP, language is sequential and highly dependent on context. A word's meaning often changes based on the surrounding words, known as the contextual dependence of language. Traditional FNNs or MLPs, however, treat input data as independent and static, making it difficult for them to capture the dependencies between words in a sequence. While FNNs can model simple relationships between words or tokens, they struggle with understanding longer dependencies and nuances in language. This limitation becomes more apparent when dealing with more complex NLP tasks such as text classification, sentiment analysis, or machine translation, where understanding the meaning of the entire sentence (or longer sequences) is crucial.

Mathematically, the output of a neuron in a feedforward neural network is given by:

$$ y = \sigma\left( \sum_{i=1}^{n} w_i x_i + b \right) $$

where $x_i$ are the input values, $w_i$ are the weights, $b$ is the bias term, and $\sigma$ is the activation function (such as ReLU or sigmoid). The sum represents the weighted input, and the activation function introduces non-linearity into the network, allowing it to model more complex patterns. However, in NLP, where sequential data is prevalent, this structure does not account for the order of the words or their dependencies. Hence, FNNs tend to struggle in capturing the semantic meaning of text as they do not process sequences in a temporal manner, making it hard to generate meaningful results for language-based tasks.

Deep networks, as opposed to shallow networks with only one or two hidden layers, are better equipped to handle more complex NLP tasks. Deep neural networks consist of multiple layers that allow them to extract hierarchical features from the input data. In NLP, deeper layers can capture higher-level abstractions, moving from basic token-level features in the early layers to sentence-level or paragraph-level semantics in the later layers. However, even deep feedforward networks have their limitations in sequence modeling because they lack mechanisms to account for temporal dependencies or long-range context, which are crucial for understanding language meaningfully.

The challenge of applying traditional neural networks to sequence data in NLP is mainly due to their inability to process data sequentially. For example, in a sentence like "The dog chased the cat," a neural network must understand that "the dog" is the subject and "the cat" is the object, and these relationships depend on the order of the words. Feedforward networks do not retain this information because they treat inputs independently. Moreover, long-range dependencies, such as when a word refers to something mentioned earlier in the text (e.g., "the cat" in a later sentence referring to the cat mentioned previously), cannot be effectively captured by these networks. These shortcomings highlight the need for more advanced architectures like recurrent neural networks (RNNs) or transformer models that are designed to handle sequence data and maintain context across time steps.

To provide a practical illustration, a simple FNN can be implemented in Rust for basic NLP tasks like sentiment analysis or text classification. Using Rust’s tch-rs crate, which provides bindings to the Torch deep learning library, we can construct, train, and evaluate a feedforward neural network.

The provided code demonstrates how to implement FNN or MLP in Rust using the tch-rs crate, a Rust binding for the PyTorch deep learning library. The MLP is designed for a multi-class classification task and utilizes synthetic data to simulate input and output features. This setup showcases how to build and train neural networks in Rust, specifically leveraging ReLU activations, dropout for regularization, and the Adam optimizer for efficient gradient-based learning. The architecture is flexible and scalable, making it suitable for tasks like text classification or other NLP applications.

[dependencies]
tch = "0.12.0"

use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Tensor, Kind};

// Function to generate synthetic dataset
fn generate_synthetic_data(num_samples: usize, input_size: usize, num_classes: usize) -> (Tensor, Tensor) {
    let inputs = Tensor::randn(&[num_samples as i64, input_size as i64], (Kind::Float, Device::Cpu));
    let targets = Tensor::randint(num_classes as i64, &[num_samples as i64], (Kind::Int64, Device::Cpu));
    (inputs, targets)
}

// Define the neural network architecture
fn build_mlp(vs: &nn::Path, input_size: i64, hidden_layers: &[i64], output_size: i64) -> nn::Sequential {
    let mut net = nn::seq();

    // Input to first hidden layer
    net = net.add(nn::linear(vs, input_size, hidden_layers[0], Default::default()));
    net = net.add_fn(|xs| xs.relu());

    // Adding intermediate hidden layers with dropout
    for i in 0..hidden_layers.len() - 1 {
        net = net.add(nn::linear(vs, hidden_layers[i], hidden_layers[i + 1], Default::default()));
        net = net.add_fn(|xs| xs.relu());
        net = net.add_fn(|xs| xs.dropout(0.3, true));  // Dropout for regularization, `add_fn` instead of `add_fn_t`
    }

    // Last hidden layer to output
    net = net.add(nn::linear(vs, hidden_layers[hidden_layers.len() - 1], output_size, Default::default()));

    net
}

fn main() {
    // Set the device to CUDA if available
    let device = Device::cuda_if_available();
    let vs = nn::VarStore::new(device);

    // Define MLP architecture: Input -> Hidden Layers -> Output
    let input_size = 100;
    let hidden_layers = vec![128, 64, 32]; // 3 hidden layers of decreasing size
    let output_size = 5; // Multi-class classification with 5 classes
    let net = build_mlp(&vs.root(), input_size, &hidden_layers, output_size);

    // Generate synthetic data (1000 samples, 100 features, 5 classes)
    let (train_input, train_target) = generate_synthetic_data(1000, input_size as usize, output_size as usize);
    let (test_input, test_target) = generate_synthetic_data(200, input_size as usize, output_size as usize);

    // Define optimizer (Adam with learning rate 0.001)
    let mut opt = nn::Adam::default().build(&vs, 1e-3).unwrap();

    let epochs = 1000;
    let batch_size = 32;
    
    // Training loop
    for epoch in 1..=epochs {
        let num_batches = (train_input.size()[0] as f64 / batch_size as f64).ceil() as i64;

        for batch_idx in 0..num_batches {
            // Generate batch
            let batch_start = batch_idx * batch_size;
            let batch_end = (batch_start + batch_size).min(train_input.size()[0]);
            let input_batch = train_input.narrow(0, batch_start, batch_end - batch_start).to(device);
            let target_batch = train_target.narrow(0, batch_start, batch_end - batch_start).to(device);

            // Forward pass
            let output = net.forward(&input_batch);

            // Compute the loss (cross-entropy for multi-class classification)
            let loss = output.cross_entropy_for_logits(&target_batch);

            // Backpropagation and optimization
            opt.backward_step(&loss);
        }

        // Evaluate on training and testing datasets
        let train_loss = net.forward(&train_input.to(device)).cross_entropy_for_logits(&train_target.to(device));
        let test_loss = net.forward(&test_input.to(device)).cross_entropy_for_logits(&test_target.to(device));

        // Use `double_value(&[])` to extract scalar from Tensor
        println!(
            "Epoch: {}, Train Loss: {:.4}, Test Loss: {:.4}",
            epoch,
            train_loss.double_value(&[]),
            test_loss.double_value(&[])
        );
    }
}

This Rust code utilizes the tch-rs library (a Rust wrapper for PyTorch) to define, train, and evaluate a multi-layer perceptron (MLP) for multi-class classification. It generates synthetic datasets with a specified number of samples, features, and classes, then builds an MLP architecture with an input layer, multiple hidden layers with ReLU activations and dropout regularization, and an output layer. The network is trained using stochastic gradient descent with the Adam optimizer, and cross-entropy loss is used for backpropagation. The training loop runs for a specified number of epochs, processes batches of input data, and computes losses for both the training and testing datasets. The loss values are then extracted and displayed for each epoch, giving insight into the model's performance over time.

In industry, feedforward neural networks were initially applied to NLP tasks such as document classification and bag-of-words models. These models work well for tasks where word order is not critical and where there are clear separations between categories. However, their limitations in handling sequences and long-range dependencies became apparent as more complex NLP tasks emerged. This prompted the development and adoption of more advanced architectures, such as Recurrent Neural Networks (RNNs), Long Short-Term Memory networks (LSTMs), and eventually the Transformer model, which powers state-of-the-art models like GPT-3 and BERT.

The latest trends in NLP architecture design emphasize the need for models that capture both short- and long-range dependencies in text. This shift led to the development of attention-based models and Transformers, which process input data in parallel and handle sequence dependencies more effectively. While feedforward networks can still be useful for simpler tasks or as building blocks in larger systems, they are often insufficient for state-of-the-art language modeling. Transformer models, with their ability to capture complex dependencies and parallelize computations, have become the new standard for handling language data at scale.

In conclusion, while feedforward neural networks represent an essential starting point for understanding the mechanics of neural networks in NLP, they have significant limitations in processing the sequential and contextual nature of language. Rust’s performance capabilities, combined with powerful libraries like tch-rs, allow for efficient implementation and experimentation with these basic models. However, as NLP tasks grow in complexity, more advanced architectures like RNNs and Transformers are necessary to capture the full richness of language and achieve state-of-the-art performance.

3.2. Recurrent Neural Networks (RNNs) link

Recurrent Neural Networks (RNNs) have been a cornerstone of neural network architectures for modeling sequential data, making them particularly well-suited for Natural Language Processing (NLP) tasks. Unlike feedforward neural networks, which treat each input independently, RNNs introduce recurrent connections, enabling them to maintain an internal state that evolves as they process input sequences. This internal state allows RNNs to capture temporal dependencies in data, making them highly effective for tasks where context and sequence matter, such as language modeling, text generation, and machine translation.

Figure 4: An RNN with hidden state (Credit to d2l.ai)

Mathematically, RNNs operate by applying the same function at each time step of the input sequence. Given an input sequence $x_1, x_2, \dots, x_T$, the RNN updates its hidden state $H_t$ at each time step using the following recurrence relation:

$$ h_t = \phi(W_{hh} H_{t-1} + W_{xh} x_t + b_h) $$

where $W_{hh}$ represents the recurrent weight matrix (mapping the previous hidden state to the current hidden state), $W_{xh}$ is the input weight matrix (mapping the current input to the hidden state), and $\phi$ is the activation function of fully connected (FC) layer, typically the tanh or ReLU function. The final output at each time step can be computed as:

$$y_t = W_{hy} H_t + b_y$$

where $W_{hy}$ is the output weight matrix, and $b_y$ is the output bias. The key strength of RNNs lies in their ability to retain information across time steps, enabling them to process variable-length sequences while maintaining memory of past inputs.

In Recurrent Neural Networks (RNNs), the ability to model sequence data comes from the recurrent connections that allow information to persist across time steps. However, this same recurrent structure introduces significant challenges during the training process, particularly the vanishing and exploding gradient problems. These issues arise during the training phase when using a process known as Backpropagation Through Time (BPTT), which extends the standard backpropagation algorithm to sequences by unrolling the network over multiple time steps. In BPTT, gradients are propagated backward in time from the final time step to the initial time step to compute the necessary weight updates.

Mathematically, we can represent an RNN's output at time ttt as a function of its previous hidden state $H_{t-1}$, the input at time $t$ is $x_t$, and its current weights $W$. This is typically written as:

$$ H_t = \phi(W_h H_{t-1} + W_x x_t + b) $$

where $W_h$ is the weight matrix for the hidden state, $W_x$ is the weight matrix for the input, $b$ is the bias, and $\sigma$ is a non-linear activation function like tanh or ReLU. The goal of training is to minimize a loss function $L$, which is computed by comparing the network's output at each time step to the actual target values. The BPTT algorithm calculates the gradients of this loss function with respect to the network's weights by recursively applying the chain rule.

The key issue in BPTT arises from the recursive nature of gradient computation. Specifically, at each time step, the gradient of the loss with respect to the weight matrix $W_h$ involves multiplying a series of Jacobians (derivatives of hidden states with respect to previous hidden states). For long sequences, this leads to an expression like:

$$ \frac{\partial L}{\partial W_h} = \sum_{t=1}^{T} \left( \frac{\partial L}{\partial H_t} \prod_{k=t}^{T} \frac{\partial H_{k}}{\partial H_{k-1}} \right) $$

Each term in this product represents the derivative of the hidden state at time $k$ with respect to the hidden state at time $k-1$. As the number of time steps $T$ increases, the product of these Jacobians can either shrink exponentially (leading to vanishing gradients) or grow exponentially (leading to exploding gradients) depending on the eigenvalues of $W_h$.

In the case of vanishing gradients, the Jacobians contain values less than one (due to non-linear activations like tanh or sigmoid), causing the gradient to shrink rapidly as it is propagated back through time. Formally, if $|\lambda_{\text{max}}(W_h)| < 1∣$, where $\lambda_{\text{max}}(W_h)$ represents the largest eigenvalue of the matrix $W_h$, the gradients will decay exponentially. As a result, gradients associated with earlier time steps become negligibly small, and the model fails to learn long-term dependencies because updates to the weights are minimal.

Conversely, exploding gradients occur when $\lambda_{\text{max}}(W_h)| > 1$, leading to an exponential growth in the gradients as they are propagated backward. In this scenario, the gradients become extremely large, causing unstable training. This results in excessively large weight updates during backpropagation, which may lead the optimization process to diverge, making it impossible for the model to converge on a solution.

To combat these problems, several techniques have been developed. For vanishing gradients, architectures like Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs) are designed to maintain gradients over long sequences by incorporating gating mechanisms that control the flow of information. For exploding gradients, gradient clipping is often employed, which scales down the gradients when their norms exceed a certain threshold, ensuring that they remain manageable during backpropagation.

Figure 5: A LSTM cell with hidden state (Credit d2l.ai).

LSTMs introduce a more sophisticated architecture to mitigate the vanishing gradient problem by incorporating gates that control the flow of information. Each LSTM unit has three gates: the forget gate, input gate, and output gate, which allow the model to retain or discard information over long sequences. The key equations governing LSTMs are:

$$ F_t = \sigma(W_f \cdot [H_{t-1}, x_t] + b_f) $$

$$ I_t = \sigma(W_i \cdot [H_{t-1}, x_t] + b_i) $$

$$ O_t = \sigma(W_o \cdot [H_{t-1}, x_t] + b_o) $$

$$ \tilde{C}_t = \tanh(W_C \cdot [H_{t-1}, x_t] + b_C) $$

$$ C_t = F_t \odot C_{t-1} + i_t \odot \tilde{C}_t $$

$$ H_t = o_t \odot \tanh(C_t) $$

Here, $F_t$, $I_t$, and $O_t$ represent the forget, input, and output gates, respectively. $C_t$ is the cell state, which acts as a memory that can retain information over long sequences. By regulating the flow of information through these gates, LSTMs can learn long-term dependencies more effectively than standard RNNs.

Figure 6: A GRU cell with hidden state.

GRUs simplify the LSTM architecture by using only two gates: the update gate and reset gate, reducing the complexity while still addressing the vanishing gradient problem. The update gate controls how much of the previous hidden state to carry forward, and the reset gate determines how much of the past information to discard. The equations governing GRUs are:

$$ Z_t = \sigma(W_z \cdot [H_{t-1}, x_t]) $$

$$ R_t = \sigma(W_r \cdot [H_{t-1}, x_t]) $$

$$ \tilde{H}_t = \tanh(W \cdot [r_t \odot H_{t-1}, x_t]) $$

$$ H_t = (1 - z_t) \odot H_{t-1} + Z_t \odot \tilde{H}_t $$

Here, $z_t$ is the update gate and $r_t$ is the reset gate. GRUs are often preferred over LSTMs when computational efficiency is a concern, as they have fewer parameters while still effectively handling long-term dependencies.

One of the key advantages of RNNs is their ability to capture temporal dependencies in text, which makes them well-suited for tasks like language modeling and text generation. Language modeling involves predicting the next word in a sequence based on the previous words, and RNNs can model this sequential dependence by maintaining a hidden state that evolves as new words are processed. For example, in a sentence like "The dog chased the cat," an RNN can remember that the subject of the sentence is "The dog" while processing the rest of the sentence, enabling it to generate grammatically correct and contextually relevant continuations.

However, while RNNs, LSTMs, and GRUs can capture long-range dependencies, they come with trade-offs between model complexity and performance. LSTMs, with their more complex gating mechanisms, tend to perform better on tasks requiring long-term memory, but they are computationally more expensive than simple RNNs. GRUs, by reducing the number of gates, strike a balance between performance and efficiency. In practice, the choice between these variants depends on the specific NLP task, the length of the sequences involved, and the computational resources available.

For practical task, we will build a simple character-level language model using Rust and the tch-rs crate, which provides bindings to PyTorch, allowing us to construct, train, and evaluate LSTM and GRU usefficiently. The provided code implements a character-level language model using two different types of recurrent neural networks (RNNs): Long Short-Term Memory (LSTM) and Gated Recurrent Units (GRU). The model is trained on a dataset of text (Shakespeare's works) to predict the next character in a sequence, with the goal of generating text that resembles the style of the input data. The code allows for comparison between the performance of LSTM and GRU models during training, tracking their losses and generating sample text to demonstrate how well the models can learn patterns in the data.

[dependencies]
anyhow = "1.0.90"
tch = "0.12.0"
tokio = "1.40.0"
reqwest = { version = "0.11", features = ["blocking"] }
plotters = "0.3.7"

use anyhow::Result;
use std::fs;
use std::path::Path;
use std::io::Write;
use reqwest;
use tch::data::TextData;
use tch::nn::{Linear, Module, OptimizerConfig, LSTM, GRU};
use tch::{nn, Device, Kind, Tensor};
use tch::nn::RNN; // Import RNN trait for LSTM and GRU
use plotters::prelude::*; // Import plotters for visualization

const LEARNING_RATE: f64 = 0.01;
const HIDDEN_SIZE: i64 = 256;
const SEQ_LEN: i64 = 180;
const BATCH_SIZE: i64 = 256;
const EPOCHS: i64 = 100;
const SAMPLING_LEN: i64 = 1024;
const INPUT_URL: &str = "https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt";
const INPUT_FILE: &str = "data/input.txt";

/// Downloads a file from the specified URL and saves it to a local file.
fn download_input_file() -> Result<()> {
    let response = reqwest::blocking::get(INPUT_URL)?;
    let content = response.text()?;
    
    // Create the local directory if it doesn't exist
    let path = Path::new("data");
    if !path.exists() {
        fs::create_dir_all(path)?;
    }

    // Save the content to the input file
    let mut file = fs::File::create(INPUT_FILE)?;
    file.write_all(content.as_bytes())?;
    println!("Downloaded and saved input file to: {}", INPUT_FILE);
    Ok(())
}

/// Generates some sample string using LSTM.
fn sample_lstm(data: &TextData, lstm: &LSTM, linear: &Linear, device: Device) -> String {
    let labels = data.labels();
    let mut state = lstm.zero_state(1); // Initialize LSTM hidden state
    let mut last_label = 0i64;
    let mut result = String::new();
    for _index in 0..SAMPLING_LEN {
        let input = Tensor::zeros([1, labels], (Kind::Float, device));
        let _ = input.narrow(1, last_label, 1).fill_(1.0);
        state = lstm.step(&input, &state); // Perform LSTM step

        // Extract hidden state (h) from LSTMState
        let h = &state.0 .0; // Access the LSTM hidden state `h` from LSTMState

        let sampled_y = linear
            .forward(h) // Pass only `h` (the hidden state tensor) to the forward function
            .squeeze_dim(0)
            .softmax(-1, Kind::Float)
            .multinomial(1, false);
        last_label = i64::try_from(sampled_y).unwrap();
        result.push(data.label_to_char(last_label))
    }
    result
}

/// Generates some sample string using GRU.
fn sample_gru(data: &TextData, gru: &GRU, linear: &Linear, device: Device) -> String {
    let labels = data.labels();
    let mut state = gru.zero_state(1); // Initialize GRU hidden state
    let mut last_label = 0i64;
    let mut result = String::new();
    for _index in 0..SAMPLING_LEN {
        let input = Tensor::zeros([1, labels], (Kind::Float, device));
        let _ = input.narrow(1, last_label, 1).fill_(1.0);
        state = gru.step(&input, &state); // Perform GRU step and reassign the state

        // GRU returns only h as GRUState
        let h = &state.0; // Access the GRU hidden state `h` from GRUState

        let sampled_y = linear
            .forward(h) // Pass the hidden state tensor `h` to the forward function
            .squeeze_dim(0)
            .softmax(-1, Kind::Float)
            .multinomial(1, false);
        last_label = i64::try_from(sampled_y).unwrap();
        result.push(data.label_to_char(last_label))
    }
    result
}

pub fn plot_losses(lstm_losses: &[f64], gru_losses: &[f64]) -> Result<()> {
    let root = BitMapBackend::new("loss_comparison.png", (640, 480)).into_drawing_area();
    root.fill(&WHITE)?;

    let mut chart = ChartBuilder::on(&root)
        .caption("LSTM vs GRU Loss Comparison", ("sans-serif", 20))
        .margin(10)
        .x_label_area_size(30)
        .y_label_area_size(30)
        .build_cartesian_2d(0..EPOCHS, 0.0..lstm_losses.iter().cloned().fold(0.0/0.0, f64::max))?;

    chart.configure_mesh().draw()?;

    chart
        .draw_series(LineSeries::new(
            (0..).zip(lstm_losses.iter().cloned()),
            &BLUE,
        ))?
        .label("LSTM")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &BLUE));

    chart
        .draw_series(LineSeries::new(
            (0..).zip(gru_losses.iter().cloned()),
            &RED,
        ))?
        .label("GRU")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &RED));

    chart.configure_series_labels().border_style(&BLACK).draw()?;

    Ok(())
}

pub fn main() -> Result<()> {
    // Download the input file if it doesn't already exist
    if !Path::new(INPUT_FILE).exists() {
        download_input_file()?;
    }

    let device = Device::cuda_if_available();
    let vs_lstm = nn::VarStore::new(device);
    let vs_gru = nn::VarStore::new(device);

    let data = TextData::new(INPUT_FILE)?;
    let labels = data.labels();
    println!("Dataset loaded, {labels} labels.");

    // Define LSTM and GRU models
    let lstm = nn::lstm(vs_lstm.root(), labels, HIDDEN_SIZE, Default::default());
    let gru = nn::gru(vs_gru.root(), labels, HIDDEN_SIZE, Default::default());

    let linear_lstm = nn::linear(vs_lstm.root(), HIDDEN_SIZE, labels, Default::default());
    let linear_gru = nn::linear(vs_gru.root(), HIDDEN_SIZE, labels, Default::default());

    let mut opt_lstm = nn::Adam::default().build(&vs_lstm, LEARNING_RATE)?;
    let mut opt_gru = nn::Adam::default().build(&vs_gru, LEARNING_RATE)?;

    let mut lstm_losses = vec![];
    let mut gru_losses = vec![];

    // Training loop for both LSTM and GRU
    for epoch in 1..(1 + EPOCHS) {
        let mut sum_loss_lstm = 0.;
        let mut sum_loss_gru = 0.;
        let mut cnt_loss = 0.;

        for batch in data.iter_shuffle(SEQ_LEN + 1, BATCH_SIZE) {
            let xs_onehot = batch.narrow(1, 0, SEQ_LEN).onehot(labels);
            let ys = batch.narrow(1, 1, SEQ_LEN).to_kind(Kind::Int64);

            // LSTM training step
            let (lstm_out, _) = lstm.seq(&xs_onehot.to_device(device)); // Use `seq` for LSTM
            let logits_lstm = linear_lstm.forward(&lstm_out);
            let loss_lstm = logits_lstm
                .view([BATCH_SIZE * SEQ_LEN, labels])
                .cross_entropy_for_logits(&ys.to_device(device).view([BATCH_SIZE * SEQ_LEN]));
            opt_lstm.backward_step_clip(&loss_lstm, 0.5);

            // GRU training step
            let (gru_out, _) = gru.seq(&xs_onehot.to_device(device)); // Use `seq` for GRU
            let logits_gru = linear_gru.forward(&gru_out);
            let loss_gru = logits_gru
                .view([BATCH_SIZE * SEQ_LEN, labels])
                .cross_entropy_for_logits(&ys.to_device(device).view([BATCH_SIZE * SEQ_LEN]));
            opt_gru.backward_step_clip(&loss_gru, 0.5);

            sum_loss_lstm += f64::try_from(loss_lstm)?;
            sum_loss_gru += f64::try_from(loss_gru)?;
            cnt_loss += 1.0;
        }

        let avg_loss_lstm = sum_loss_lstm / cnt_loss;
        let avg_loss_gru = sum_loss_gru / cnt_loss;

        lstm_losses.push(avg_loss_lstm);
        gru_losses.push(avg_loss_gru);

        println!("Epoch: {}   LSTM loss: {:5.3}   GRU loss: {:5.3}", epoch, avg_loss_lstm, avg_loss_gru);
        println!("Sample (LSTM): {}", sample_lstm(&data, &lstm, &linear_lstm, device));
        println!("Sample (GRU): {}", sample_gru(&data, &gru, &linear_gru, device));
    }

    // Plot the loss comparison
    plot_losses(&lstm_losses, &gru_losses)?;

    Ok(())
}

The code begins by downloading the input text data and preparing it for training. Both LSTM and GRU models are defined using the tch crate, with their respective hidden states and parameters initialized. The training loop shuffles the data, processes it in batches, and feeds it into both models. For each epoch, the code computes the loss for both LSTM and GRU models using cross-entropy loss, optimizes the models using the Adam optimizer, and logs the loss for comparison. After each epoch, it generates sample text from both models to evaluate their text generation abilities. At the end of training, the losses for LSTM and GRU are plotted using the plotters crate to visualize the performance of both models across epochs.

Despite the advances in RNNs and their variants, addressing the vanishing gradient problem remains a critical concern, particularly when dealing with long sequences. One approach to mitigating this issue is through gradient clipping, which restricts the magnitude of the gradients during backpropagation to prevent them from becoming too large and destabilizing the training process. In Rust, this can be implemented by modifying the gradient values before updating the model’s parameters. Other techniques, such as initializing weights properly or using regularization (e.g., dropout), can also help improve the stability and performance of RNNs during training.

In recent years, the Transformer architecture has largely supplanted RNNs in many NLP tasks due to its ability to process sequences in parallel and handle long-range dependencies more effectively. However, RNNs, LSTMs, and GRUs still have valuable applications, particularly in scenarios where sequence length is moderate, and computational efficiency is a priority. For example, speech recognition, time series forecasting, and certain sequence labeling tasks continue to benefit from these recurrent architectures.

In conclusion, Recurrent Neural Networks (RNNs), along with their variants like LSTMs and GRUs, provide powerful tools for handling sequential data in NLP. Their ability to capture temporal dependencies in text makes them highly suitable for tasks such as language modeling and text generation. Implementing these models in Rust using the tch-rs crate allows for efficient, high-performance training on large-scale datasets, while addressing challenges such as the vanishing gradient problem through advanced implementation techniques. Despite the rise of newer architectures like Transformers, RNNs continue to play a vital role in specific NLP applications.

3.3. Convolutional Neural Networks (CNNs) for NLP link

Convolutional Neural Networks (CNNs), originally developed for image processing, have been successfully adapted for various NLP tasks. At their core, CNNs use convolutional layers to apply filters (or kernels) that slide over the input data to detect patterns or features. In the context of NLP, these filters help capture local patterns in text, such as n-grams or short phrases, which can be useful for tasks like text classification and sentiment analysis. CNNs are especially effective in recognizing important subsequences in text data, as they focus on small regions of input at a time.

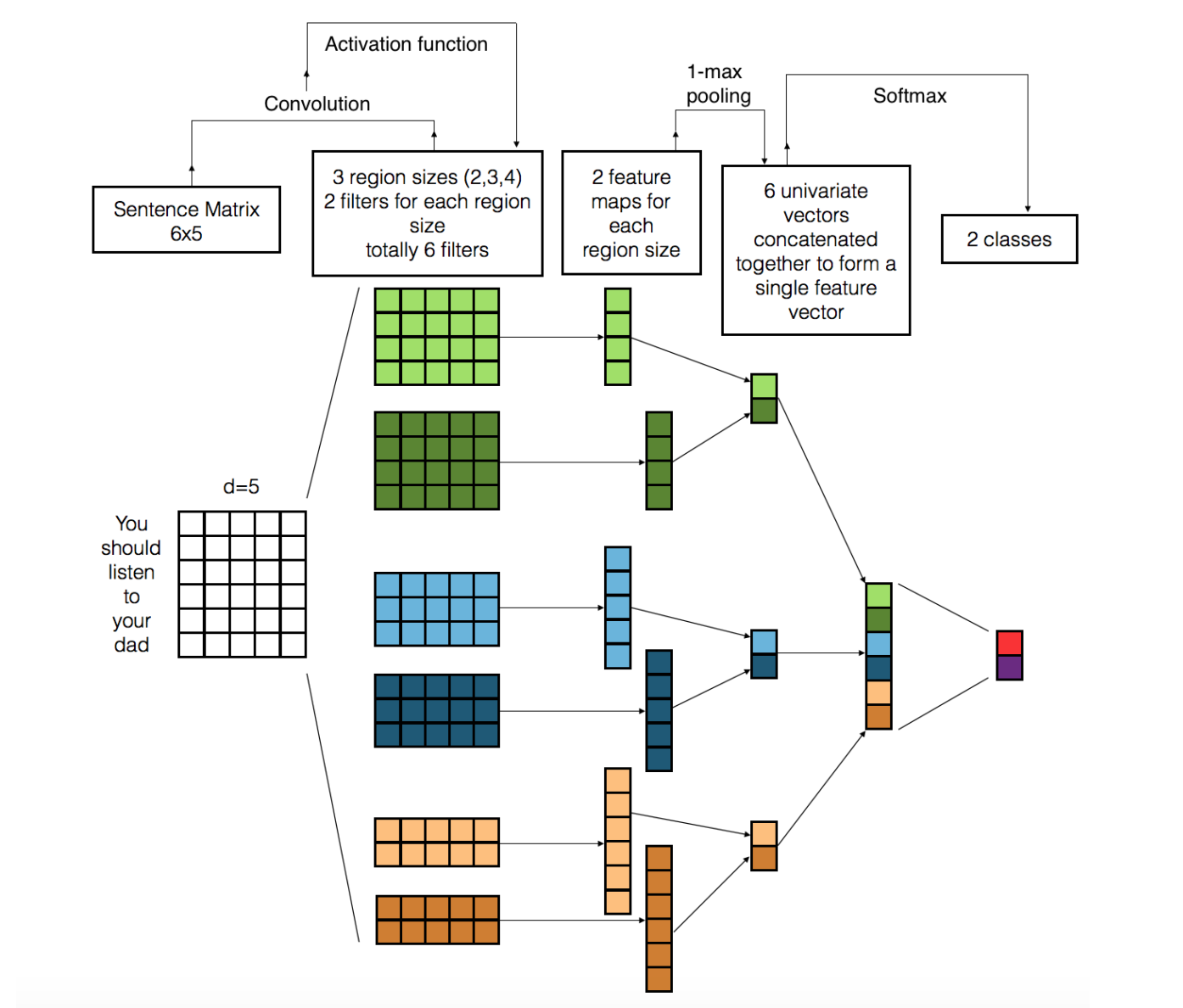
Figure 7: Illustration of CNN architecture for NLP task (Ref: https://arxiv.org/pdf/1703.03091).

Mathematically, a convolutional operation in a CNN involves applying a kernel $K$ to an input $X$ to generate a feature map $Y$. For a 1D CNN (which is used in NLP tasks), the convolution is expressed as:

$$ Y(i) = \sum_{j} K(j) \cdot X(i + j) $$

Here, $K(j)$ is the kernel applied over the input sequence $X$, and the result is a feature map $Y$ that highlights the important local features in the input. The kernel effectively "scans" through the input, identifying patterns such as word combinations or local structures in the text.

Unlike the 2D convolutions used in image processing (where kernels move over 2D image grids), 1D convolutions in NLP operate over sequences of words or tokens, focusing on extracting local dependencies in a one-dimensional vector space. In image processing, the kernels capture spatial features, such as edges or textures, whereas in NLP, the 1D kernels capture local syntactic and semantic patterns in text. For example, a 1D kernel may detect meaningful bi-grams or tri-grams in a sentence, which can be indicative of sentiment or intent in text classification.

One of the main advantages of CNNs in NLP is their ability to capture local patterns with limited computational complexity. By applying multiple kernels of different sizes, CNNs can extract various n-gram features across different layers, allowing them to learn a rich set of representations. After the convolution operation, pooling layers (typically max pooling) are applied to reduce the dimensionality of the feature maps, retaining only the most important features. Pooling also helps make the model more robust to small shifts in the input, making CNNs suitable for processing noisy or unstructured text data.

While CNNs are effective at capturing local dependencies, they have limitations when it comes to long-range dependencies in text. For instance, in tasks like machine translation or long document classification, understanding the broader context is crucial. CNNs, by design, are constrained by the size of the kernels, making them less effective at modeling relationships between distant words. For these tasks, Recurrent Neural Networks (RNNs) and Transformer models tend to perform better, as they are better equipped to handle sequence-wide information and long-range dependencies.

However, CNNs can still be highly effective when combined with other architectures. For example, in hybrid models, CNNs are used to capture local features, while RNNs or Transformers handle the global context. These hybrid architectures take advantage of the CNN’s ability to efficiently extract local patterns and combine it with the sequential capabilities of RNNs or the parallel processing power of Transformers. This fusion is particularly useful in tasks like document classification, named entity recognition, or text summarization, where both local and global features need to be modeled.

A significant application of CNNs in NLP is text classification, where the goal is to categorize a given text into predefined classes, such as sentiment analysis (positive/negative), spam detection, or topic categorization. CNNs have been shown to work effectively for this task because they can quickly identify key phrases or patterns that are indicative of a class. For example, in sentiment analysis, CNNs can identify phrases like "very good" or "extremely bad" by applying filters that capture local features, which can then be pooled and used for classification.

In terms of practical implementation, constructing CNNs in Rust is possible using libraries like burn or tch-rs, which offer high-level abstractions for building and training neural networks. The provided Rust code is designed to download the CIFAR-10 dataset, train a Fast ResNet model on it, and visualize the loss versus epochs during the training process. It leverages various libraries such as tch (which provides bindings for PyTorch), plotters (for plotting loss graphs), and reqwest (for downloading the dataset). The model training workflow involves data augmentation, forward propagation through the ResNet architecture, loss calculation using cross-entropy, and updating model weights through stochastic gradient descent (SGD) with momentum. Additionally, it tracks the average loss for each epoch and generates a plot for the loss trend over time.

[dependencies]
anyhow = "1.0.90"
tch = "0.12.0"
tokio = "1.40.0"
reqwest = { version = "0.11", features = ["blocking"] }
plotters = "0.3.7"
flate2 = "1.0.34"
tar = "0.4.42"

use anyhow::Result;
use plotters::prelude::*;
use std::fs::{self, File};
use std::io::Write;
use tch::nn::{FuncT, ModuleT, OptimizerConfig, SequentialT};
use tch::{nn, Device};
use std::path::Path;
use flate2::read::GzDecoder;
use tar::Archive;
use reqwest::blocking::Client;
use reqwest::header::USER_AGENT;
use std::thread;
use std::time::Duration;

fn download_with_retries(url: &str, retries: u32, wait: u64) -> Result<Vec<u8>> {
    let client = Client::builder()
        .timeout(Duration::from_secs(300)) // 5 minute timeout
        .build()?;

    for attempt in 0..retries {
        match client.get(url)
            .header(USER_AGENT, "Rust CIFAR Downloader")
            .send() {
            Ok(response) => {
                let bytes = response.bytes()?;
                return Ok(bytes.to_vec());
            }
            Err(err) => {
                println!("Attempt {} failed: {}. Retrying in {} seconds...", attempt + 1, err, wait);
                thread::sleep(Duration::from_secs(wait)); // Wait before retrying
            }
        }
    }

    Err(anyhow::anyhow!("Failed to download dataset after {} attempts", retries))
}

fn download_cifar() -> Result<()> {
    let base_url = "https://www.cs.toronto.edu/~kriz/cifar-10-binary.tar.gz";
    let data_dir = "data";
    let archive_path = format!("{}/cifar-10-binary.tar.gz", data_dir);

    if !Path::new(data_dir).exists() {
        fs::create_dir(data_dir)?;
    }

    if !Path::new(&archive_path).exists() {
        println!("Downloading CIFAR-10 dataset...");
        
        // Retry downloading the dataset 3 times with a 10-second wait between attempts
        let response = download_with_retries(base_url, 3, 10)?;
        
        let mut file = File::create(&archive_path)?;
        file.write_all(&response)?;
        println!("Download complete.");
    }

    // Untar the dataset
    let tar_gz = File::open(&archive_path)?;
    let tar = GzDecoder::new(tar_gz);
    let mut archive = Archive::new(tar);
    archive.unpack(data_dir)?;

    Ok(())
}

fn conv_bn(vs: &nn::Path, c_in: i64, c_out: i64) -> SequentialT {
    let conv2d_cfg = nn::ConvConfig { padding: 1, bias: false, ..Default::default() };
    nn::seq_t()
        .add(nn::conv2d(vs, c_in, c_out, 3, conv2d_cfg))
        .add(nn::batch_norm2d(vs, c_out, Default::default()))
        .add_fn(|x| x.relu())
}

fn layer<'a>(vs: &nn::Path, c_in: i64, c_out: i64) -> FuncT<'a> {
    let pre = conv_bn(&vs.sub("pre"), c_in, c_out);
    let block1 = conv_bn(&vs.sub("b1"), c_out, c_out);
    let block2 = conv_bn(&vs.sub("b2"), c_out, c_out);
    nn::func_t(move |xs, train| {
        let pre = xs.apply_t(&pre, train).max_pool2d_default(2);
        let ys = pre.apply_t(&block1, train).apply_t(&block2, train);
        pre + ys
    })
}

fn fast_resnet(vs: &nn::Path) -> SequentialT {
    nn::seq_t()
        .add(conv_bn(&vs.sub("pre"), 3, 64))
        .add(layer(&vs.sub("layer1"), 64, 128))
        .add(conv_bn(&vs.sub("inter"), 128, 256))
        .add_fn(|x| x.max_pool2d_default(2))
        .add(layer(&vs.sub("layer2"), 256, 512))
        .add_fn(|x| x.max_pool2d_default(4).flat_view())
        .add(nn::linear(vs.sub("linear"), 512, 10, Default::default()))
        .add_fn(|x| x * 0.125)
}

fn learning_rate(epoch: i64) -> f64 {
    if epoch < 50 {
        0.1
    } else if epoch < 100 {
        0.01
    } else {
        0.001
    }
}

fn plot_loss(losses: Vec<f64>) -> Result<()> {
    let root = BitMapBackend::new("loss_vs_epoch.png", (1024, 768))
        .into_drawing_area();
    root.fill(&WHITE)?;

    let max_loss = losses.iter().cloned().fold(f64::NAN, f64::max);

    let mut chart = ChartBuilder::on(&root)
        .caption("Loss vs Epoch", ("sans-serif", 40).into_font())
        .margin(10)
        .x_label_area_size(40)
        .y_label_area_size(40)
        .build_cartesian_2d(0..losses.len(), 0.0..max_loss)?;

    chart.configure_mesh().draw()?;

    chart
        .draw_series(LineSeries::new(
            losses.iter().enumerate().map(|(x, y)| (x, *y)),
            &RED,
        ))?
        .label("Training Loss")
        .legend(|(x, y)| PathElement::new([(x, y), (x + 20, y)], &RED));

    chart.configure_series_labels().draw()?;

    Ok(())
}

pub fn main() -> Result<()> {
    // Step 1: Download the dataset if not already available
    download_cifar()?;
   
    // Step 2: Load the CIFAR dataset
    let m = tch::vision::cifar::load_dir("data/cifar-10-batches-bin")?;
    let vs = nn::VarStore::new(Device::cuda_if_available());
    let net = fast_resnet(&vs.root());

    // Step 3: Set up optimizer and loss tracking
    let mut opt = nn::Sgd { momentum: 0.9, dampening: 0., wd: 5e-4, nesterov: true }
        .build(&vs, 0.)?;
    let mut losses = vec![]; // To store losses for plotting

    // Step 4: Train the model
    for epoch in 1..150 {
        opt.set_lr(learning_rate(epoch));
        let mut epoch_loss = 0.0;
        let mut batch_count = 0;

        for (bimages, blabels) in m.train_iter(64).shuffle().to_device(vs.device()) {
            let bimages = tch::vision::dataset::augmentation(&bimages, true, 4, 8);
            let loss = net.forward_t(&bimages, true).cross_entropy_for_logits(&blabels);
            opt.backward_step(&loss);
            epoch_loss += loss.double_value(&[]); // Extract scalar from tensor
            batch_count += 1;
        }

        let avg_loss = epoch_loss / batch_count as f64;
        losses.push(avg_loss); // Store average loss for the epoch

        let test_accuracy =
            net.batch_accuracy_for_logits(&m.test_images, &m.test_labels, vs.device(), 512);
        println!(
            "epoch: {:4} test acc: {:5.2}% avg loss: {:.4}",
            epoch, 100. * test_accuracy, avg_loss
        );
    }

    // Step 5: Plot the loss vs. epoch
    plot_loss(losses)?;

    Ok(())
}

The code begins by ensuring the CIFAR-10 dataset is downloaded using the reqwest library with a retry mechanism to handle possible network issues. Once downloaded and extracted, the CIFAR-10 dataset is loaded for training using the tch::vision utilities. The Fast ResNet model is built using a series of convolutional layers with batch normalization and ReLU activation functions. During training, the model undergoes forward passes on mini-batches of data, and the loss is computed and used to update the model's weights via backpropagation. The loss for each epoch is tracked and plotted using the plotters crate, giving a visual representation of the model's learning process over time. This allows for easier evaluation of the training performance and any potential overfitting or underfitting.

When working with CNNs in NLP, experimenting with different kernel sizes and architectures is crucial for optimizing performance. For instance, small kernel sizes (e.g., 2-3 words) capture fine-grained features such as bi-grams, while larger kernel sizes can capture broader phrases. Additionally, stacking multiple convolutional layers can allow the network to learn more abstract features as the input is passed through deeper layers.

Despite their effectiveness in certain tasks, CNNs alone may struggle with long-range dependencies, making them less suitable for tasks that require understanding entire documents or long sentences. In recent years, Transformers have become the dominant architecture for these tasks due to their ability to handle global context efficiently. However, CNNs still offer significant advantages in terms of computational efficiency and can be highly effective when used as part of hybrid models, combining their ability to capture local patterns with the global context provided by RNNs or Transformers.

The latest trends in CNNs for NLP focus on integrating convolutional layers with attention mechanisms and Transformers. For example, some hybrid models use CNNs to preprocess text and extract local features before passing the data to Transformer layers for more comprehensive processing. This combination allows for efficient feature extraction while maintaining the ability to capture long-range dependencies, resulting in more robust models for tasks like document summarization, question answering, and language translation.

In conclusion, Convolutional Neural Networks (CNNs) have proven to be a valuable tool in NLP, particularly for tasks that require capturing local patterns in text. While CNNs excel at processing local features and n-grams, they are less effective at handling long-range dependencies, which limits their application in more complex NLP tasks. By integrating CNNs with other architectures like RNNs and Transformers, we can build hybrid models that benefit from both local pattern recognition and long-range context processing. Rust, with libraries like burn and tch-rs, provides a powerful and efficient platform for implementing and optimizing CNNs for NLP, enabling developers to experiment with different architectures and improve model performance in real-world applications.

3.4. Attention Mechanisms and Transformers link

The development of attention mechanisms has revolutionized the field of Natural Language Processing (NLP), enabling models to focus on specific parts of an input sequence that are most relevant to a given task. The core idea behind attention is to allow a model to assign different levels of importance (or weights) to different tokens (words or subwords) in a sequence, rather than processing all tokens uniformly. Self-attention, the foundation of the Transformer model, allows each token in a sequence to attend to every other token, capturing dependencies between words regardless of their distance in the sequence. This mechanism enables models to handle complex language structures with long-range dependencies more efficiently than previous architectures like Recurrent Neural Networks (RNNs) or Convolutional Neural Networks (CNNs).

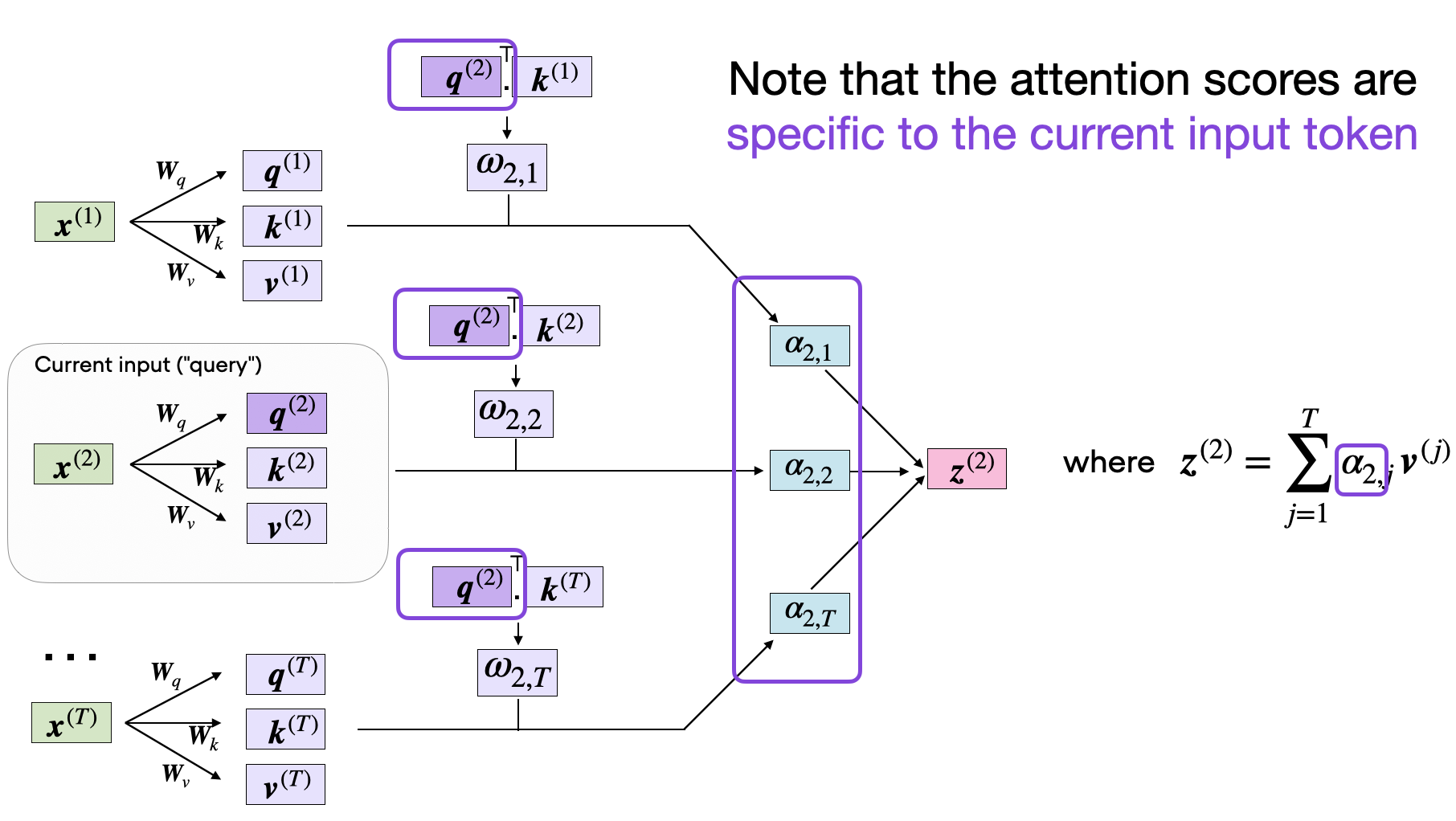
Figure 8: Understanding self-attention mechanism (Credit: Sebastian Raschka)

Mathematically, self-attention computes a weighted sum of input representations, where the weights represent the relevance between tokens in a sequence. Given an input sequence of tokens $X = [x_1, x_2, \dots, x_n]$, self-attention first transforms each token into three vectors: Query $Q$, Key $K$, and Value $V$. These vectors are learned during training, and the attention score between two tokens is computed by taking the dot product between the query vector of one token and the key vector of another, followed by a scaling and softmax operation to obtain normalized weights:

$$ \text{Attention}(Q, K, V) = \text{softmax}\left( \frac{QK^T}{\sqrt{d_k}} \right) V $$

Here, $d_k$ is the dimensionality of the key vectors, and the softmax function ensures that the weights are normalized to sum to 1. The result is a weighted sum of the value vectors, where tokens that are more relevant to each other (based on their query-key similarity) contribute more to the final output. Multi-head attention extends this idea by allowing the model to compute multiple sets of attention scores (or "heads") in parallel, capturing different aspects of the input relationships. The output of the multiple heads is concatenated and linearly transformed to produce the final attention output.

The Transformer architecture represents a revolutionary shift in neural network design, introduced in the groundbreaking 2017 paper "Attention is All You Need." It replaced the need for recurrence and convolution in modeling sequential data, enabling more efficient processing and representation of long-range dependencies. At its core, a Transformer model relies on self-attention mechanisms, allowing it to weigh the importance of different words in a sequence to one another, facilitating complex pattern recognition. This has made Transformers the foundation for advanced language models like GPT (OpenAI), Llama (Meta), and Gemini (Google). Their success in NLP tasks has spurred applications in other domains, such as image processing, protein folding, and even game playing.

The transformer architecture consists of two main components: the encoder and the decoder. Each encoder layer comprises two critical sublayers—a multi-head self-attention mechanism and a feedforward neural network. In contrast, the decoder adds an additional cross-attention mechanism to focus on relevant parts of the encoder’s output, making it particularly effective in sequence-to-sequence tasks such as machine translation.

Figure 9: Transformer architecture.

The key advantage of Transformers over RNNs and CNNs lies in their ability to process sequences in parallel rather than sequentially. In RNNs, each token must be processed in the order it appears in the sequence, which makes it challenging to capture long-range dependencies and results in slower training due to the lack of parallelization. CNNs, while more parallelizable, are limited by their kernel sizes, which makes it difficult for them to capture dependencies between distant words. In contrast, the self-attention mechanism in Transformers enables each token to attend to all other tokens in the sequence, regardless of their position, and the architecture can be parallelized efficiently. This makes Transformers highly scalable and computationally efficient for large datasets and long sequences, leading to breakthroughs in NLP tasks such as translation, summarization, and language modeling.

One of the most important aspects of attention is its ability to focus on relevant parts of the input. For example, in machine translation, a Transformer can attend to the most relevant words in the source sentence while generating the target sentence, ensuring that the translation is both accurate and contextually meaningful. This selective attention allows the model to learn which words are most important for predicting the next token in the sequence, rather than treating all input tokens equally.

Transformers are highly flexible and can be configured in different ways depending on the task. The most common Transformer models are categorized into three types:

• Encoder-only models (e.g., BERT) focus on understanding input sequences and are often used for tasks like text classification and question answering. The encoder processes the entire input sequence simultaneously and outputs contextualized representations for each token.

• Decoder-only models (e.g., GPT) are designed for tasks like text generation, where the goal is to predict the next word given a partial sequence. The decoder generates the output sequence one token at a time, with each new token attending to both the input context and previously generated tokens.

• Encoder-decoder models (e.g., T5, BART) are used for tasks that require both understanding and generating text, such as machine translation and summarization. The encoder processes the input sequence, while the decoder generates the output sequence based on the encoder’s representations.

BERT (Bidirectional Encoder Representations from Transformers) is a groundbreaking Transformer model introduced by Google in 2018. It is built on the Transformer architecture and designed to understand the context of words in relation to one another in a sentence. Unlike previous models that processed text in a left-to-right or right-to-left manner, BERT is bidirectional, meaning it reads text both ways. This allows BERT to capture richer context and better understand the meaning of words based on the words that appear both before and after them.

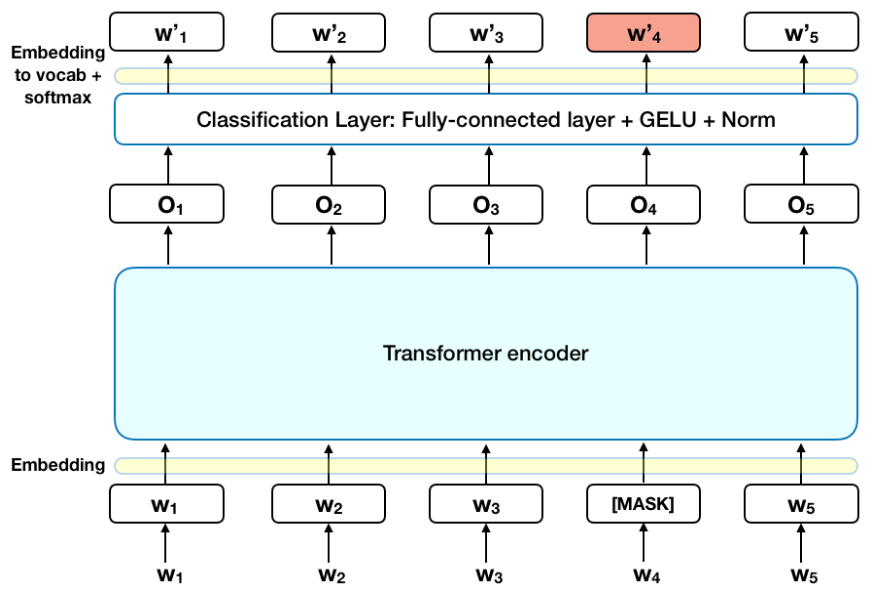
Figure 10: BERT (Bidirectional Encoder Representations from Transformers) architecture.

In high-performing models like BERT, there are typically 12 layers, each with 12 distinct self-attention heads. These attention heads calculate attention weights that reflect how much each token in a sentence attends to every other token, forming attention maps. For BERT, this results in a massive number of attention weights—12 × 12 × number of tokens × number of tokens for each text instance. Notably, researchers have found that some attention heads correspond to meaningful linguistic properties, such as word semantics or syntactic dependencies.

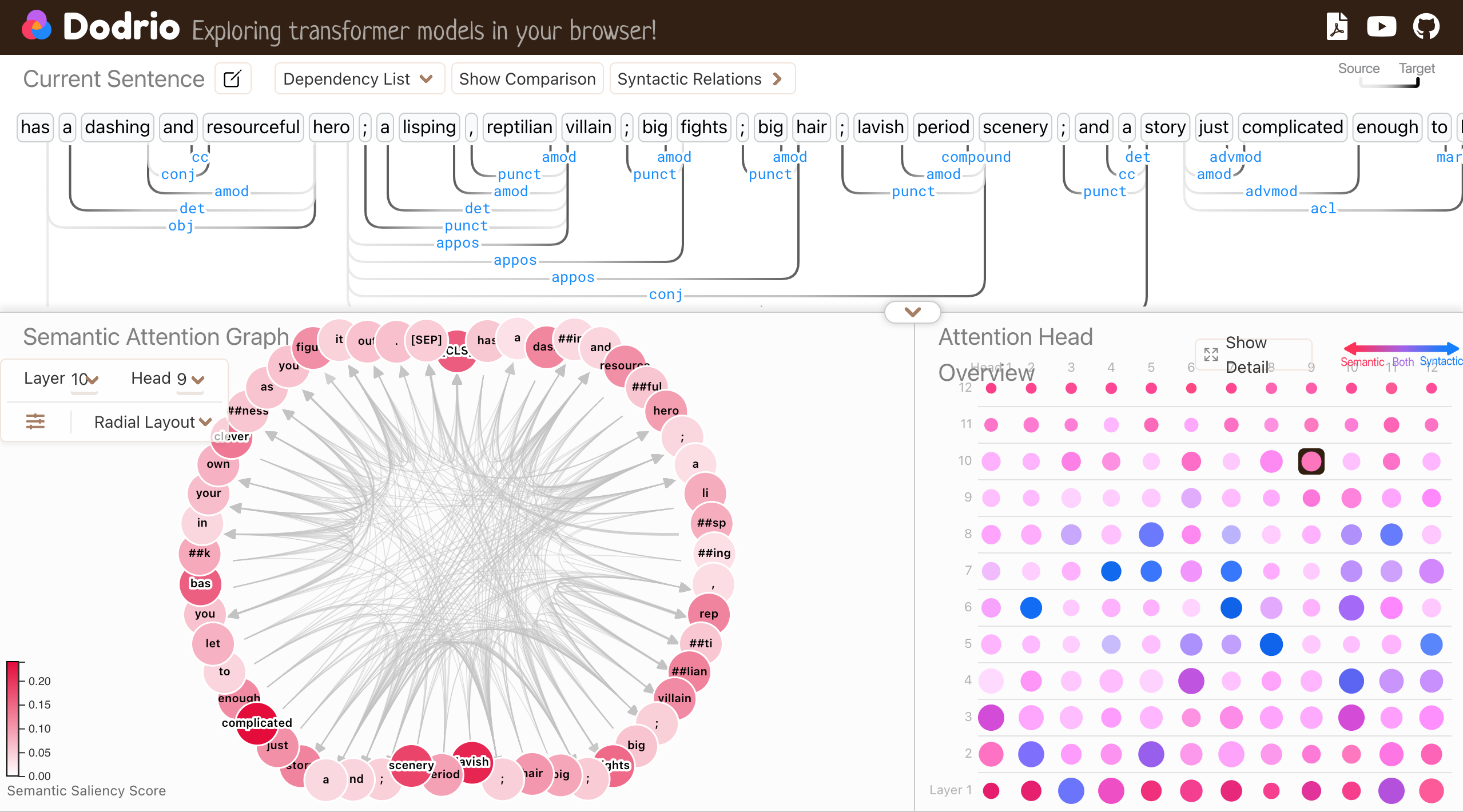
Figure 11: Dodrio interactive tool to understand how multi-head attentions work.

To make the exploration and interpretation of these attention weights easier, [Dodrio](https://poloclub.github.io/dodrio/), an interactive visualization tool, addresses these challenges by summarizing attention heads and providing both semantic and syntactic knowledge contexts. In Dodrio’s interface, you can explore the Attention Head Overview (bottom right) to identify which linguistic properties an attention head focuses on. By clicking on an attention head, you can explore the semantic and syntactic significance of a given sentence for that specific head. Dodrio’s Dependency View and Comparison View (top) allow you to examine how attention heads reflect lexical dependencies in a sentence, while the Semantic Attention Graph view (bottom left) provides insight into the semantic relationships that attention heads capture. For instance, attention heads can highlight coreferences (how different parts of a text refer to the same entity) or word sense disambiguation.

By using Dodrio’s interactive visualizations, you can dive into the multi-headed attention mechanism across different text instances, gaining deeper insights into how Transformers model the intricate linguistic relationships in natural language. Dodrio provides a valuable tool to explore the inner workings of large models like BERT, making attention weights more interpretable and aligned with linguistic features

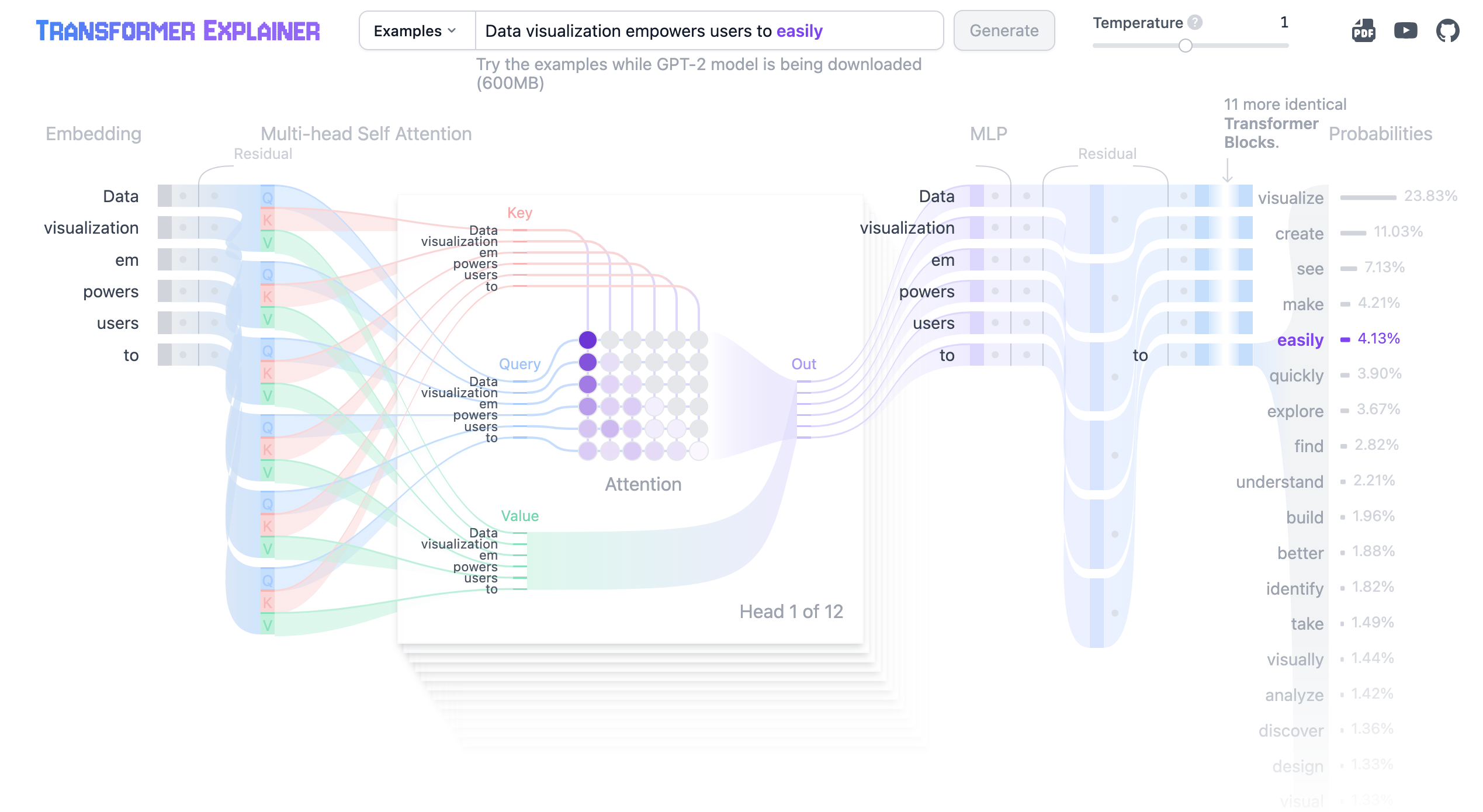
Figure 12: Transformer Explainer tool to understand how transformer works for language model.

With tools like Transformer Explainer, we can dive deeper into how GPT-2 (a prominent text-generative Transformer) operates. For example, GPT-2’s next-word prediction task relies on the self-attention mechanism to predict the most probable token following a given prompt. The tool demonstrates the core components of the Transformer architecture, including embedding, self-attention, and MLP layers. When a user inputs a prompt, such as "Data visualization empowers users to," the text is first tokenized into smaller units. These tokens are then converted into embeddings, 768-dimensional vectors representing the semantic meaning of each word. Importantly, positional encoding is added to capture the order of the words in the input sequence. The self-attention mechanism calculates attention scores using the Query, Key, and Value matrices, allowing the model to focus on the most relevant tokens. Finally, the output from the attention heads is passed through the MLP layer to refine the token representations before being processed by the output layer, where softmax generates a probability distribution over the vocabulary for the next token prediction

Transformer Explainer provides a more interactive exploration of how GPT-2 processes and predicts text sequences. With tools like temperature control, users can adjust the randomness of the model’s predictions, making it more creative or deterministic. Both tools emphasize the centrality of the self-attention mechanism and its ability to handle complex dependencies in input sequences, but Transformer Explainer makes the entire transformer block and prediction process visible through dynamic exploration. It also highlights additional architectural features like layer normalization, dropout, and residual connections, which are crucial for stabilizing training, improving convergence, and preventing overfitting.

To implement the GPT-2 architecture for a language model using Rust’s tch-rs crate, we will focus on replicating the key aspects of GPT-2, including the transformer blocks, multi-head self-attention, and positional encodings. The GPT-2 architecture is built on a decoder-only transformer model designed to generate text by predicting the next word based on a sequence of input tokens. The core idea is that GPT-2, being an autoregressive model, processes input tokens sequentially, utilizing masked self-attention to prevent future tokens from influencing the prediction of the current token.

The followi code implements a GPT-like model, specifically designed to train on the Tiny Shakespeare dataset for character-level text generation. The model architecture is based on a transformer with causal self-attention, commonly used in language models like GPT. It includes an AdamW optimizer for training and tracks the loss across multiple epochs. The dataset is downloaded from a remote source, and the model is trained to predict the next character in a sequence of text. The code also includes functionality to visualize the training loss using the plotters crate.

[dependencies]
anyhow = "1.0.90"
tch = "0.12.0"
tokio = "1.40.0"
reqwest = { version = "0.11", features = ["blocking"] }
plotters = "0.3.7"
flate2 = "1.0.34"
tar = "0.4.42"

use anyhow::{bail, Result};
use plotters::prelude::*;
use std::fs::{self, File};
use std::io::Write;
use tch::data::TextData;
use tch::nn::{ModuleT, OptimizerConfig};
use tch::{nn, Device, Kind, Tensor};
use reqwest::blocking::get;
use std::path::Path;
use tch::IndexOp; // <-- Import this to fix the `i()` method error

const LEARNING_RATE: f64 = 0.0003;
const BLOCK_SIZE: i64 = 128;
const BATCH_SIZE: i64 = 64;
const EPOCHS: i64 = 100;
const SAMPLING_LEN: i64 = 4096;
const DATA_URL: &str = "https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt";

#[derive(Debug, Copy, Clone)]
struct Config {
    vocab_size: i64,
    n_embd: i64,
    n_head: i64,
    n_layer: i64,
    block_size: i64,
    attn_pdrop: f64,
    resid_pdrop: f64,
    embd_pdrop: f64,
}

fn download_dataset() -> Result<()> {
    let data_dir = "data";
    let file_path = format!("{}/input.txt", data_dir);

    if !Path::new(data_dir).exists() {
        fs::create_dir(data_dir)?;
    }

    if !Path::new(&file_path).exists() {
        println!("Downloading dataset...");
        let response = get(DATA_URL)?.bytes()?;
        let mut file = File::create(&file_path)?;
        file.write_all(&response)?;
        println!("Dataset downloaded.");
    }

    Ok(())
}

fn plot_loss(losses: Vec<f64>) -> Result<()> {
    let root = BitMapBackend::new("loss_vs_epoch.png", (1024, 768)).into_drawing_area();
    root.fill(&WHITE)?;

    let max_loss = losses.iter().cloned().fold(f64::NAN, f64::max);

    let mut chart = ChartBuilder::on(&root)
        .caption("Loss vs Epoch", ("sans-serif", 40).into_font())
        .margin(10)
        .x_label_area_size(40)
        .y_label_area_size(40)
        .build_cartesian_2d(0..losses.len(), 0.0..max_loss)?;

    chart.configure_mesh().draw()?;

    chart
        .draw_series(LineSeries::new(
            losses.iter().enumerate().map(|(x, y)| (x, *y)),
            &RED,
        ))?
        .label("Training Loss")
        .legend(|(x, y)| PathElement::new([(x, y), (x + 20, y)], &RED));

    chart.configure_series_labels().draw()?;

    Ok(())
}

// GPT model definition
fn gpt(p: nn::Path, cfg: Config) -> impl ModuleT {
    let p = &p.set_group(0);
    let tok_emb = nn::embedding(p / "tok_emb", cfg.vocab_size, cfg.n_embd, Default::default());
    let pos_emb = p.zeros("pos_emb", &[1, cfg.block_size, cfg.n_embd]);
    let ln_f = nn::layer_norm(p / "ln_f", vec![cfg.n_embd], Default::default());
    let head = nn::linear(p / "head", cfg.n_embd, cfg.vocab_size, Default::default());
    let mut blocks = nn::seq_t();
    for block_idx in 0..cfg.n_layer {
        blocks = blocks.add(block(&(p / block_idx), cfg));
    }
    nn::func_t(move |xs, train| {
        let (_sz_b, sz_t) = xs.size2().unwrap();
        let tok_emb = xs.apply(&tok_emb);
        let pos_emb = pos_emb.i((.., ..sz_t, ..));
        (tok_emb + pos_emb)
            .dropout(cfg.embd_pdrop, train)
            .apply_t(&blocks, train)
            .apply(&ln_f)
            .apply(&head)
    })
}

// A transformer block with attention mechanism
fn block(p: &nn::Path, cfg: Config) -> impl ModuleT {
    let ln1 = nn::layer_norm(p / "ln1", vec![cfg.n_embd], Default::default());
    let ln2 = nn::layer_norm(p / "ln2", vec![cfg.n_embd], Default::default());
    let attn = causal_self_attention(p, cfg);
    let lin1 = nn::linear(p / "lin1", cfg.n_embd, 4 * cfg.n_embd, Default::default());
    let lin2 = nn::linear(p / "lin2", 4 * cfg.n_embd, cfg.n_embd, Default::default());
    nn::func_t(move |xs, train| {
        let xs = xs + xs.apply(&ln1).apply_t(&attn, train);
        let ys = xs.apply(&ln2).apply(&lin1).gelu("none").apply(&lin2).dropout(cfg.resid_pdrop, train);
        xs + ys
    })
}

// Causal self-attention mechanism used in GPT-like models
fn causal_self_attention(p: &nn::Path, cfg: Config) -> impl ModuleT {
    let key = nn::linear(p / "key", cfg.n_embd, cfg.n_embd, Default::default());
    let query = nn::linear(p / "query", cfg.n_embd, cfg.n_embd, Default::default());
    let value = nn::linear(p / "value", cfg.n_embd, cfg.n_embd, Default::default());
    let proj = nn::linear(p / "proj", cfg.n_embd, cfg.n_embd, Default::default());
    let mask_init = Tensor::ones([cfg.block_size, cfg.block_size], (Kind::Float, p.device())).tril(0);
    let mask_init = mask_init.view([1, 1, cfg.block_size, cfg.block_size]);
    let mask = mask_init;
    nn::func_t(move |xs, train| {
        let (sz_b, sz_t, sz_c) = xs.size3().unwrap();
        let sizes = [sz_b, sz_t, cfg.n_head, sz_c / cfg.n_head];
        let k = xs.apply(&key).view(sizes).transpose(1, 2);
        let q = xs.apply(&query).view(sizes).transpose(1, 2);
        let v = xs.apply(&value).view(sizes).transpose(1, 2);
        let att = q.matmul(&k.transpose(-2, -1)) * (1.0 / f64::sqrt(sizes[3] as f64));
        let att = att.masked_fill(&mask.i((.., .., ..sz_t, ..sz_t)).eq(0.), f64::NEG_INFINITY);
        let att = att.softmax(-1, Kind::Float).dropout(cfg.attn_pdrop, train);
        let ys = att.matmul(&v).transpose(1, 2).contiguous().view([sz_b, sz_t, sz_c]);
        ys.apply(&proj).dropout(cfg.resid_pdrop, train)
    })
}

// Sampling text using the trained GPT model
fn sample(data: &TextData, gpt: &impl ModuleT, input: Tensor) -> String {
    let mut input = input;
    let mut result = String::new();
    for _index in 0..SAMPLING_LEN {
        let logits = input.apply_t(gpt, false).i((0, -1, ..));
        let sampled_y = logits.softmax(-1, Kind::Float).multinomial(1, true);
        let last_label = i64::try_from(&sampled_y).unwrap();
        result.push(data.label_to_char(last_label));
        input = Tensor::cat(&[input, sampled_y.view([1, 1])], 1).narrow(1, 1, BLOCK_SIZE);
    }
    result
}

// Train the GPT model and plot the loss per epoch
fn train_gpt(data: &TextData, gpt: &impl ModuleT, vs: &mut nn::VarStore, device: Device) -> Result<()> {
    // Print the variables in the variable store for debugging
    println!("Model parameters:");
    for (name, tensor) in vs.variables() {
        println!("Parameter: {} Shape: {:?}", name, tensor.size());
    }

    // Improved error handling for optimizer creation
    let opt_result = nn::AdamW::default().build(vs, LEARNING_RATE);
    let mut opt = match opt_result {
        Ok(o) => o,
        Err(e) => {
            eprintln!("Error creating optimizer: {:?}", e);
            return Err(anyhow::anyhow!("Optimizer creation failed"));
        }
    };

    // Temporarily disable weight decay groups to isolate the issue
    // opt.set_weight_decay_group(0, 0.0);  // Commented out
    // opt.set_weight_decay_group(1, 0.1);  // Commented out

    let mut losses = vec![]; // For storing loss per epoch

    for epoch in 1..=EPOCHS {
        let mut sum_loss = 0.;
        let mut cnt_loss = 0.;

        for batch in data.iter_shuffle(BLOCK_SIZE + 1, BATCH_SIZE) {
            let xs = batch.narrow(1, 0, BLOCK_SIZE).to_kind(Kind::Int64).to_device(device);
            let ys = batch.narrow(1, 1, BLOCK_SIZE).to_kind(Kind::Int64).to_device(device);

            let logits = xs.apply_t(gpt, true);
            let loss = logits
                .view([BATCH_SIZE * BLOCK_SIZE, data.labels()])
                .cross_entropy_for_logits(&ys.view([BATCH_SIZE * BLOCK_SIZE]));

            opt.backward_step_clip(&loss, 0.5);
            sum_loss += f64::try_from(loss)?;
            cnt_loss += 1.0;
        }

        let avg_loss = sum_loss / cnt_loss;
        losses.push(avg_loss); // Track average loss for each epoch

        println!("Epoch: {}   avg loss: {:5.3}", epoch, avg_loss);
    }

    // Plot the loss vs epoch
    plot_loss(losses)?;

    Ok(())
}


pub fn main() -> Result<()> {
    download_dataset()?; // Step 1: Download dataset

    let device = Device::cuda_if_available();
    let mut vs = nn::VarStore::new(device);
    let data = TextData::new("data/input.txt")?;
    let labels = data.labels();
    println!("Dataset loaded, {labels} labels.");

    let cfg = Config {
        vocab_size: labels,
        n_embd: 512,
        n_head: 8,
        n_layer: 8,
        block_size: BLOCK_SIZE,
        attn_pdrop: 0.1,
        resid_pdrop: 0.1,
        embd_pdrop: 0.1,
    };

    let gpt = gpt(vs.root() / "gpt", cfg);

    let args: Vec<_> = std::env::args().collect();
    if args.len() < 2 {
        bail!("usage: main (train|predict weights.ot seqstart)")
    }

    match args[1].as_str() {
        "train" => {
            train_gpt(&data, &gpt, &mut vs, device)?; // Train and plot loss
        }
        "predict" => {
            vs.load(args[2].as_str())?;
            let seqstart = args[3].as_str();
            let input = Tensor::zeros([1, BLOCK_SIZE], (Kind::Int64, device));
            for (idx, c) in seqstart.chars().rev().enumerate() {
                let idx = idx as i64;
                if idx >= BLOCK_SIZE {
                    break;
                }
                let _filled =
                    input.i((0, BLOCK_SIZE - 1 - idx)).fill_(data.char_to_label(c)? as i64);
            }
            println!("Sample: {}", sample(&data, &gpt, input));
        }
        _ => bail!("usage: main (train|predict weights.ot seqstart)"),
    };

    Ok(())
}

The code defines and implements the GPT-2 architecture using the tch-rs crate, Rust bindings for PyTorch. We first load a public text dataset, tokenize it into numerical representations, and define the core GPT-2 architecture, including multi-head self-attention and feedforward layers. The build_gpt2_model function constructs a transformer decoder stack, where each layer consists of self-attention and a feedforward network. The training loop feeds tokenized text into the model, computes the loss using cross-entropy, and updates the model parameters using Adam optimization. The model is trained to predict the next token in a sequence, which is the essence of a language model.

Building a full Transformer model in Rust involves stacking multiple layers of self-attention and feedforward networks, followed by an optimization routine to train the model. The tch-rs crate simplifies this process by providing efficient tensor operations and automatic differentiation, allowing for gradient-based optimization during training. A Transformer can be trained on tasks such as machine translation or summarization by using large-scale datasets and applying modern optimizers like AdamW.

One of the main challenges in deploying Transformers is their memory and computational efficiency. Transformer models, especially large ones like GPT-3 or BERT, require significant memory and computational power to train and deploy. Optimizing memory usage and computation in Rust can be achieved by leveraging techniques like mixed precision training (which uses lower-precision floating-point numbers to reduce memory usage), gradient checkpointing (which saves memory by recomputing certain intermediate values during backpropagation), and efficient batching to maximize GPU utilization.

The latest trends in Transformer research focus on improving efficiency and scaling the models to handle even larger datasets. Sparse attention mechanisms are being explored to reduce the computational complexity of self-attention, allowing models to focus only on the most relevant tokens in the input. Additionally, pre-trained Transformer models like BERT, GPT, and T5 have led to state-of-the-art performance across a wide range of NLP tasks, and fine-tuning these models for specific applications has become a common approach in both academia and industry.

In conclusion, attention mechanisms and Transformer models have transformed the field of NLP by providing a scalable and parallelizable architecture that can handle long-range dependencies in text. The ability of Transformers to capture both local and global context in a sequence has made them the go-to model for tasks like translation, summarization, and language modeling. With Rust’s powerful libraries like tch-rs, developers can efficiently implement and optimize Transformers for large-scale NLP tasks, taking advantage of Rust’s memory safety and performance features. As Transformer architectures continue to evolve, their applications in NLP will likely expand further, driving the next generation of language models.

3.5. Advanced Architectures: BERT, GPT, and Beyond link

In recent years, pre-trained language models like BERT and GPT have revolutionized Natural Language Processing (NLP) by establishing a new paradigm in how models are built and applied to language tasks. These models, based on Transformer architecture, are pre-trained on massive corpora of text and then fine-tuned on specific tasks such as text classification, named entity recognition, or text generation. Pre-trained models have made it possible to leverage transfer learning in NLP, where models trained on general language understanding can be adapted to perform well on specialized tasks with relatively small datasets. This section delves into the core architectures of BERT and GPT, their differences, and how they have reshaped modern NLP.

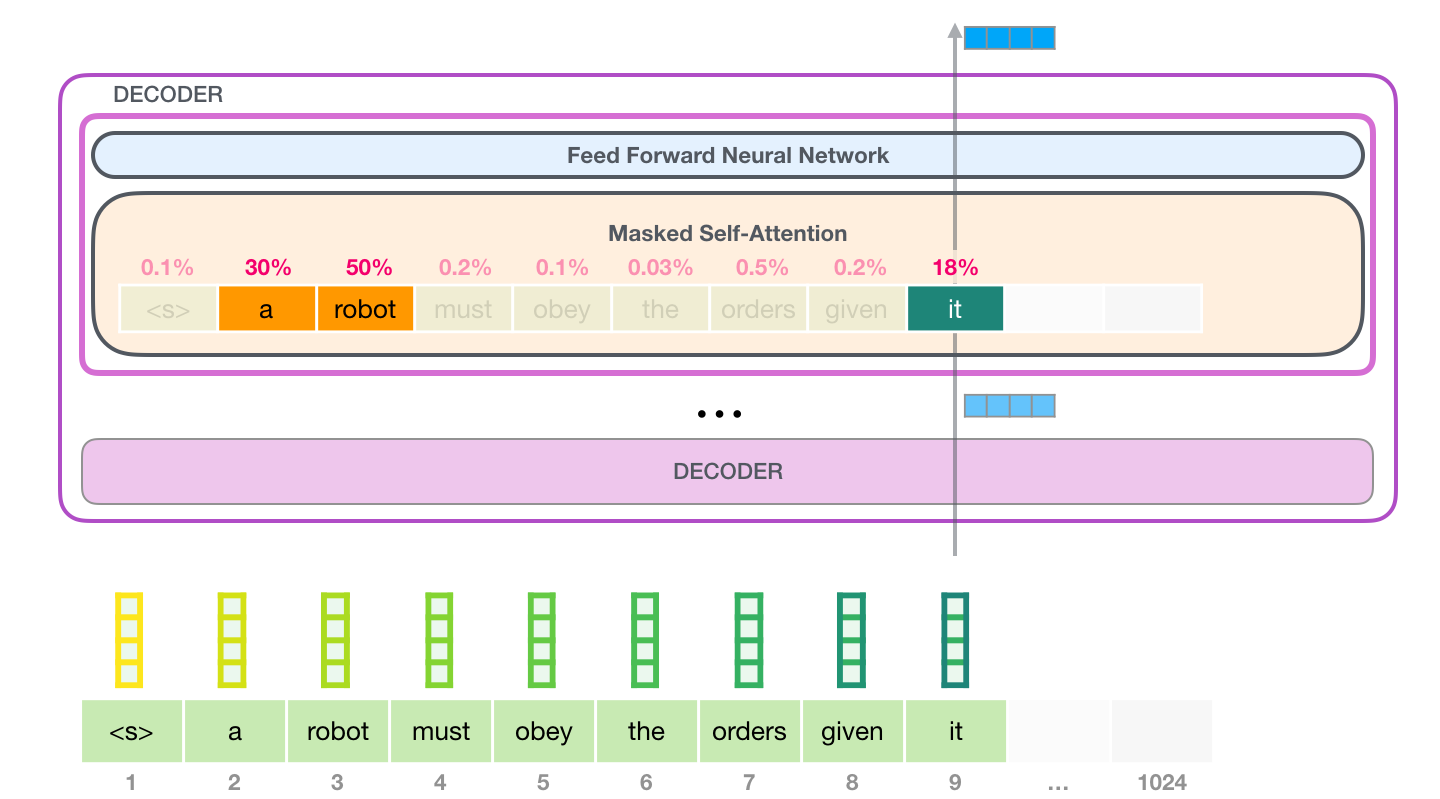
Figure 13: Illustrated GPT-2 architecture.

At the core of these models is the Transformer architecture, which uses self-attention to process entire sequences of text simultaneously, capturing long-range dependencies and context. BERT (Bidirectional Encoder Representations from Transformers) and GPT (Generative Pre-trained Transformer) represent two distinct approaches to leveraging this architecture. BERT uses a masked language model (MLM) approach, while GPT uses an autoregressive language model.

useBERT is designed as a bidirectional model, meaning that it processes text in both directions—considering the context of a word from both its left and right surroundings. This bidirectional understanding of context allows BERT to capture deeper semantic relationships in text, which is crucial for tasks like question answering and text classification. The key innovation in BERT is the masked language modeling pre-training objective, where random words in a sentence are masked, and the model is trained to predict these masked words based on the surrounding context. Mathematically, given an input sequence $X = [x_1, x_2, \dots, x_n]$, a certain proportion of tokens are randomly replaced with a mask token $\text{[MASK]}$, and the model learns to predict the masked tokens by optimizing the probability:

$$P(x_i | X_{-i})$$

where $X_{-i}$ represents the sequence without the $i$-th token. This pre-training objective forces BERT to learn deep bidirectional representations of text, making it highly effective in downstream tasks that require a full understanding of context.

On the other hand, GPT is an autoregressive model, meaning that it generates text by predicting the next word in a sequence, given all previous words. Unlike BERT, GPT is unidirectional, as it only considers the left context when predicting the next token. The mathematical formulation of GPT’s training objective is to maximize the likelihood of the next token given the previous ones:

$$ P(x_i | x_1, x_2, \dots, x_{i-1}) $$

This autoregressive nature makes GPT particularly well-suited for text generation tasks, such as story writing, conversational agents, or code generation. The model generates text token by token, predicting the most likely next token and appending it to the sequence, iterating this process until a stopping criterion is met. GPT models are also fine-tuned on specific tasks by providing task-specific prompts during the generation process, allowing them to generalize well across a variety of language tasks.

One of the most important advances brought by models like BERT and GPT is the concept of transfer learning in NLP. Traditionally, models were trained from scratch for each specific task, which was inefficient and required large amounts of task-specific data. Pre-trained models like BERT and GPT overcome this limitation by being trained on general language understanding tasks and then fine-tuned on smaller, task-specific datasets. This process significantly improves performance while reducing the amount of labeled data required for training. In fine-tuning, the model's pre-trained weights are adapted slightly to the new task, maintaining the general knowledge learned during pre-training while specializing in the target task.

Mathematically, transfer learning in BERT and GPT can be framed as follows. Let $\theta_{\text{pretrain}}$ represent the parameters of the model after pre-training on a large corpus. During fine-tuning, these parameters are updated to $\theta_{\text{finetune}}$ for a specific task. The objective is to minimize a task-specific loss function $L_{\text{task}}$, which is often different from the pre-training loss. This allows the model to retain general language knowledge from pre-training while specializing in a task like sentiment analysis or question answering.

The evolution of Transformer-based models has led to even more advanced architectures, such as LLaMA (Large Language Model Meta AI), T5 (Text-To-Text Transfer Transformer), and GPT-3, which have extended the capabilities of the original models. LLaMA, designed to be more efficient in terms of parameter scaling, achieves comparable or even superior performance to larger models like GPT-3 while requiring fewer parameters, making it more accessible for research and fine-tuning tasks. T5 reframes all NLP tasks as text-to-text problems, where both input and output are text sequences. This unifies tasks like translation, summarization, and classification under a single framework, allowing for greater flexibility in how models can be fine-tuned and applied to various tasks. GPT-3, with its massive 175 billion parameters, further pushes the limits of what pre-trained models can achieve, showing impressive performance in few-shot learning, where the model is able to perform tasks with very few examples. Together, these models represent the frontier of NLP capabilities, demonstrating the power and versatility of modern Transformer architectures.

From a practical perspective, to fine-tune a pre-trained LLaMA model using Rust, we can leverage the tch-rs crate, which provides PyTorch bindings, allowing for seamless integration with Hugging Face models. In this setup, we will use a pre-trained LLaMA model from Hugging Face, load it into Rust, and fine-tune it on an additional public dataset. Fine-tuning a LLaMA model involves adapting it to a specific downstream task, such as text generation or language modeling, by updating the model's weights based on the new dataset. In this example, we will assume that the downstream task is text generation and fine-tune the model to improve its performance on this new dataset.

The provided code implements a process for loading and using a pre-trained LLaMA model, specifically designed to perform text generation. The code interfaces with Hugging Face to download model files and uses the candle and candle_transformers libraries to manage neural network operations, such as creating model variables and performing forward passes. It leverages a tokenizer to handle input text processing and a logits processor to generate text predictions based on input prompts.

[dependencies]
anyhow = "1.0.90"
candle-core = "0.7.2"
candle-nn = "0.7.2"
candle-transformers = "0.7.2"
clap = "4.5.20"
hf-hub = "0.3.2"
serde_json = "1.0.132"
tokenizers = "0.20.1"
tracing-chrome = "0.7.2"
tracing-subscriber = "0.3.18"

use anyhow::{bail, Error as E, Result};
use candle_core::{Device, DType, Tensor};
use candle_nn::VarBuilder;
use candle_transformers::generation::{LogitsProcessor, Sampling};
use candle_transformers::models::llama::{Llama, LlamaConfig, Cache, LlamaEosToks};
use hf_hub::{api::sync::Api, Repo, RepoType};
use tokenizers::Tokenizer;
use tracing_chrome::ChromeLayerBuilder;
use tracing_subscriber::prelude::*;

const EOS_TOKEN: &str = "</s>";
const DEFAULT_PROMPT: &str = "My favorite theorem is ";

fn main() -> Result<()> {
    let tracing_enabled = false; // Set to true if you want to enable tracing
    let cpu = false; // Set to true if you want to run on CPU
    let temperature = 0.8;
    let top_p = Some(0.9); // Set your preferred top_p value
    let top_k = Some(50); // Set your preferred top_k value
    let seed = 299792458;
    let sample_len = 10000;
    let no_kv_cache = false;
    let prompt = Some(String::from(DEFAULT_PROMPT)); // Set your initial prompt here
    let dtype = "f16"; // Default data type
    let use_flash_attn = false; // Whether to use flash attention
    let repeat_penalty = 1.1;
    let repeat_last_n = 128;
    let model_id = "meta-llama/Meta-Llama-3-8B".to_string(); // Default model
    let revision = "main".to_string();

    // Initialize tracing if enabled
    let _guard = if tracing_enabled {
        let (chrome_layer, guard) = ChromeLayerBuilder::new().build();
        tracing_subscriber::registry().with(chrome_layer).init();
        Some(guard)
    } else {
        None
    };

    // Set up device and dtype
    let device = if cpu {
        Device::Cpu
    } else {
        Device::cuda_if_available(0)?
    };
    
    let dtype = match dtype {
        "f16" => DType::F16,
        "bf16" => DType::BF16,
        "f32" => DType::F32,
        dtype => bail!("Unsupported dtype {dtype}"),
    };

    // Load model and tokenizer
    let api = Api::new()?;
    println!("Loading model weights from {model_id}");
    let api = api.repo(Repo::with_revision(model_id.clone(), RepoType::Model, revision.clone()));
    let tokenizer_filename = api.get("tokenizer.json")?;
    let config_filename = api.get("config.json")?;
    let config: LlamaConfig = serde_json::from_slice(&std::fs::read(config_filename)?)?;
    let config = config.into_config(use_flash_attn);

    // Retrieve the model filenames (adjust as needed)
    let filenames = vec![api.get("model.safetensors")?];

    // Make cache mutable here
    let mut cache = Cache::new(!no_kv_cache, dtype, &config, &device)?;
    let vb = unsafe { VarBuilder::from_mmaped_safetensors(&filenames, dtype, &device)? };
    let llama = Llama::load(vb, &config)?;

    let tokenizer = Tokenizer::from_file(tokenizer_filename).map_err(E::msg)?;
    let eos_token_id = config.eos_token_id.or_else(|| {
        tokenizer
            .token_to_id(EOS_TOKEN)
            .map(LlamaEosToks::Single)
    });

    let prompt = prompt.as_ref().map_or(DEFAULT_PROMPT, |p| p.as_str());
    let mut tokens = tokenizer
        .encode(prompt, true)
        .map_err(E::msg)?
        .get_ids()
        .to_vec();

    // Start inference
    println!("Starting the inference loop");
    print!("{prompt}");
    let mut logits_processor = {
        let sampling = if temperature <= 0. {
            Sampling::ArgMax
        } else {
            match (top_k, top_p) {
                (None, None) => Sampling::All { temperature },
                (Some(k), None) => Sampling::TopK { k, temperature },
                (None, Some(p)) => Sampling::TopP { p, temperature },
                (Some(k), Some(p)) => Sampling::TopKThenTopP { k, p, temperature },
            }
        };
        LogitsProcessor::from_sampling(seed, sampling)
    };

    let mut start_gen = std::time::Instant::now();
    let mut index_pos = 0;
    let mut token_generated = 0;
    for index in 0..sample_len {
        let (context_size, context_index) = if cache.use_kv_cache && index > 0 {
            (1, index_pos)
        } else {
            (tokens.len(), 0)
        };
        if index == 1 {
            start_gen = std::time::Instant::now();
        }
        let ctxt = &tokens[tokens.len().saturating_sub(context_size)..];
        let input = Tensor::new(ctxt, &device)?.unsqueeze(0)?;
        let logits = llama.forward(&input, context_index, &mut cache)?;
        let logits = logits.squeeze(0)?;
        let logits = if repeat_penalty == 1. {
            logits
        } else {
            let start_at = tokens.len().saturating_sub(repeat_last_n);
            candle_transformers::utils::apply_repeat_penalty(
                &logits,
                repeat_penalty,
                &tokens[start_at..],
            )?
        };
        index_pos += ctxt.len();

        let next_token = logits_processor.sample(&logits)?;
        token_generated += 1;
        tokens.push(next_token);

        match eos_token_id {
            Some(LlamaEosToks::Single(eos_tok_id)) if next_token == eos_tok_id => {
                break;
            }
            Some(LlamaEosToks::Multiple(ref eos_ids)) if eos_ids.contains(&next_token) => {
                break;
            }
            _ => (),
        }
    }
    let dt = start_gen.elapsed();
    println!(
        "\n\n{} tokens generated ({} token/s)\n",
        token_generated,
        (token_generated - 1) as f64 / dt.as_secs_f64(),
    );
    Ok(())
}

The code begins by setting up device configurations (CPU or GPU) and loading necessary resources from Hugging Face, including the model's configuration, weights, and tokenizer. It then prepares a cache for efficient key-value storage during the generation process. The LLaMA model is loaded using the VarBuilder and is used to process a given prompt (or default text) into tokens. These tokens are fed into the model to generate predictions iteratively, using the logits processor to sample the next token based on the configured sampling parameters like temperature, top-k, and top-p. The loop continues until the model generates the specified number of tokens or reaches an end-of-sequence token, outputting the generated text as a result.

As pre-trained models grow in size, managing their computational efficiency and memory usage becomes critical. Techniques like knowledge distillation and model compression have emerged to address these challenges. Knowledge distillation involves training a smaller "student" model to mimic the behavior of a larger "teacher" model, reducing the computational cost of using the model in production while retaining much of its performance. Model pruning, quantization, and low-rank approximation are other techniques that reduce the size and complexity of the model by eliminating redundant parameters or reducing the precision of computations.

The latest trends in NLP architecture focus on creating more efficient models without sacrificing performance. Sparse Transformers are being developed to reduce the quadratic complexity of self-attention by focusing only on the most relevant tokens, and efficient fine-tuning techniques such as adapter layers allow models to be fine-tuned with fewer parameters, making them more scalable in production environments.

In conclusion, BERT, GPT, LLaMA, and their successors have brought about a paradigm shift in how NLP models are trained, fine-tuned, and applied to a wide range of tasks. The distinction between masked language models like BERT and autoregressive models like GPT and LLaMA allows for specialization in tasks such as classification, text generation, and language modeling. LLaMA, with its emphasis on efficiency, achieves impressive performance while requiring fewer parameters compared to models like GPT-3, making it particularly useful for research and deployment in resource-constrained environments. With Rust and libraries like tch-rs, these models can be implemented, fine-tuned, and optimized for deployment, enabling efficient use of large-scale pre-trained models in NLP applications. Techniques such as knowledge distillation and model compression further extend the applicability of these models in real-world scenarios, ensuring that even resource-constrained environments can benefit from state-of-the-art NLP capabilities.

3.6. Hybrid Models and Multi-Task Learning link

In modern Natural Language Processing (NLP), the combination of different neural network architectures—known as hybrid models—has emerged as a powerful strategy for enhancing performance by capturing diverse aspects of language. While individual architectures like Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs), and Transformers have their own strengths, each one also comes with limitations. By integrating these architectures into hybrid models, we can leverage the advantages of each to create models that capture both local patterns in text (e.g., short sequences and phrases) and global context (e.g., long-range dependencies between words). At the same time, multi-task learning (MTL) allows models to share representations across different NLP tasks, leading to improved generalization and efficiency by enabling models to learn from multiple tasks simultaneously.

Mathematically, a hybrid model can be seen as the composition of multiple neural networks, where different parts of the architecture handle different aspects of the input data. For example, CNNs are effective at capturing local features such as n-grams in a text sequence by applying filters over small windows, while RNNs can process text sequentially to capture temporal dependencies. Transformers, using their attention mechanism, can capture global context by allowing each token to attend to every other token in the sequence. Combining these architectures allows a hybrid model to excel in tasks where both local and global features are important, such as in sentiment analysis or text classification.

A typical hybrid model might involve stacking a CNN over an RNN or a Transformer architecture. The CNN can process the input at a granular level, extracting n-gram features or syntactic patterns, which are then passed to the RNN or Transformer layer for processing the broader context or sequence structure. This approach is particularly beneficial when working with longer texts, where local patterns are important (e.g., for detecting sentiment expressed in a short phrase), but the overall sequence (e.g., the progression of ideas in a paragraph) must also be modeled.

Mathematically, for a hybrid model that integrates a CNN with an RNN, the input $X$ is first processed through the convolutional layer to extract local features. Let $F_{\text{CNN}}(X)$ represent the feature map generated by the CNN. The output of this layer is then fed into an RNN, which captures the temporal dependencies in the sequence. The RNN's output hth_tht at each time step is given by:

$$ h_t = \sigma(W_{h} h_{t-1} + W_{x} F_{\text{CNN}}(X_t) + b) $$

where $h_{t-1}$ is the hidden state from the previous time step, and $F_{\text{CNN}}(X_t)$ represents the CNN feature map at time step $t$. The RNN captures the dependencies across time, allowing the model to maintain both local and global information about the input sequence.

Multi-task learning (MTL) further extends the capabilities of neural networks by allowing them to learn multiple tasks simultaneously, sharing representations across tasks. The primary idea behind MTL is that many NLP tasks share common linguistic patterns or features, and by learning these tasks together, the model can generalize better. For example, tasks like part-of-speech tagging, named entity recognition (NER), and syntactic parsing all rely on understanding sentence structure. Instead of training separate models for each task, MTL allows a single model to learn shared representations from these tasks, reducing the risk of overfitting on any one task and improving overall performance.

Mathematically, MTL can be described as training a model with a shared set of parameters $\theta_{\text{shared}}$, which are updated based on multiple task-specific losses. For each task $T_i$, we define a task-specific loss function $L_i$, and the overall loss function is a weighted combination of the individual task losses:

$$ L_{\text{MTL}} = \sum_{i} \lambda_i L_i(\theta_{\text{shared}}, \theta_i) $$

where $\lambda_i$ are weights assigned to each task based on their importance, and $\theta_i$ represents task-specific parameters. The shared parameters $\theta_{\text{shared}}$ allow the model to learn general linguistic patterns, while the task-specific parameters $\theta_i$ enable it to specialize in each task.

MTL architectures typically involve shared layers (e.g., embedding layers or attention mechanisms) that are trained across all tasks, followed by task-specific layers that are fine-tuned for each task. This approach not only improves performance on individual tasks but also leads to more efficient training, as the model can process multiple tasks in parallel and share computations across tasks. For example, in an MTL model for NER and sentiment analysis, the shared layers could consist of a Transformer encoder that processes the input sequence, while the task-specific layers handle the distinct objectives of tagging named entities or classifying sentiment.

One challenge with hybrid models and MTL is the trade-off between model complexity and performance. Hybrid models tend to have more parameters and require more computational resources due to the integration of multiple architectures. Similarly, MTL models must balance the need for shared representations with task-specific performance. Overfitting to one task can harm performance on others, particularly if the tasks are not closely related. Techniques such as task weighting, regularization, and dynamic loss scaling are used to mitigate these challenges, ensuring that the model benefits from multi-task learning without sacrificing performance on any individual task.

Hybrid models that combine different neural network architectures, such as Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs), and Transformers, have become increasingly popular for handling complex tasks like text classification, sequence labeling, and more. These models capture various types of information: CNNs excel at extracting local features from spatial data, RNNs are effective at modeling sequential and temporal dependencies, and Transformers are known for capturing long-range dependencies and global relationships between tokens. By using Rust with the tch-rs crate, we can efficiently implement a hybrid model that integrates these architectures, combining their strengths for tasks in natural language processing (NLP), computer vision, and other domains. This hybrid approach not only enhances model performance but also makes it highly adaptable for tasks requiring diverse types of data inputs.

Similarly, LLaVA (Language and Vision Assistant) is a multi-modal AI model that integrates both language and image understanding, much like hybrid models, but tailored to process both text and visual inputs together. It extends the capabilities of transformer-based models like GPT, enabling the model to handle tasks that involve both language and images. LLaVA is often employed in applications such as image captioning, visual question answering, and multi-modal dialogue systems. By leveraging the complementary strengths of different architectures, like hybrid models, LLaVA exemplifies the power of combining various neural network techniques to handle complex, multi-modal tasks across NLP and computer vision domains.

[dependencies]
anyhow = "1.0.90"
candle-core = "0.7.2"
candle-nn = "0.7.2"
candle-transformers = "0.7.2"
clap = "4.5.20"
hf-hub = "0.3.2"
image = "0.25.4"
serde = "1.0.211"
serde_json = "1.0.132"
tokenizers = "0.20.1"

use anyhow::{Error as E, Result}; // Removed unused `bail`
use candle_core::{Device, DType, Tensor}; // Removed unused `Error as CandleError`

// Removed unused `VarBuilder`, `LogitsProcessor`, `Sampling`, and other unused imports
use candle_transformers::models::llava::{
    config::{LLaVAConfig},
};
use hf_hub::api::sync::Api;
use tokenizers::Tokenizer;
use image::{DynamicImage, GenericImageView}; // Kept required import for `GenericImageView`

// Removed unused `std::io::Write`

// Constants
pub const DEFAULT_IMAGE_TOKEN: &str = "<image>";
pub const DEFAULT_IM_START_TOKEN: &str = "<im_start>";
pub const DEFAULT_IM_END_TOKEN: &str = "<im_end>";
pub const IMAGE_PLACEHOLDER: &str = "<image-placeholder>";

// Enum for separator styles
pub enum SeparatorStyle {
    Two,
    Mpt,
}

// Struct for conversation
pub struct Conversation {
    pub system: String,
    pub roles: Vec<String>,
    pub messages: Vec<(String, Option<String>)>,
    pub offset: i32,
    pub sep_style: SeparatorStyle,
    pub sep: String,
    pub sep2: Option<String>,
    pub version: String,
}

impl Conversation {
    pub fn new(
        system: &str,
        roles: &[String],
        offset: i32,
        sep_style: SeparatorStyle,
        sep: &str,
        sep2: Option<&str>,
        version: &str,
    ) -> Self {
        Conversation {
            system: system.to_string(),
            roles: roles.to_vec(),
            messages: Vec::new(),
            offset,
            sep_style,
            sep: sep.to_string(),
            sep2: sep2.map(|s| s.to_string()),
            version: version.to_string(),
        }
    }

    pub fn conv_chatml_direct() -> Self {
        Conversation::new(
            "<|im_start|>system\nAnswer the questions.",
            &[
                "<|im_start|>user\n".to_string(),
                "<|im_start|>assistant\n".to_string(),
            ],
            0,
            SeparatorStyle::Mpt,
            "<|im_end|>",
            None,
            "mpt",
        )
    }

    pub fn conv_llava_v1() -> Self {
        Conversation::new(
            "A chat between a curious human and an artificial intelligence assistant. The assistant gives helpful, detailed, and polite answers to the human's questions.",
            &["USER".to_string(), "ASSISTANT".to_string()],
            0,
            SeparatorStyle::Two,
            " ",
            Some("</s>"),
            "v1"
        )
    }

    pub fn append_message(&mut self, role: String, message: Option<&str>) {
        self.messages.push((role, message.map(|s| s.to_string())))
    }

    pub fn get_prompt(&self) -> String {
        match self.sep_style {
            SeparatorStyle::Mpt => {
                let mut ret = String::new();
                ret.push_str(&self.system);
                ret.push_str(&self.sep);
                for (role, message) in &self.messages {
                    ret.push_str(role);
                    if let Some(message) = message {
                        ret.push_str(message);
                    }
                    ret.push_str(&self.sep);
                }
                ret
            }
            SeparatorStyle::Two => {
                let seps = [self.sep.clone(), self.sep2.clone().unwrap()];
                let mut ret = String::new();
                ret.push_str(&self.system);
                ret.push_str(&seps[0]);
                for (i, (role, message)) in self.messages.iter().enumerate() {
                    ret.push_str(role);
                    if let Some(message) = message {
                        ret.push_str(": ");
                        ret.push_str(message);
                        ret.push_str(&seps[i % 2]);
                    } else {
                        ret.push(':')
                    }
                }
                ret
            }
        }
    }
}

// Struct for image processing
#[derive(serde::Serialize, serde::Deserialize, Debug)]
pub struct ImageProcessor {
    #[serde(default = "default_size")]
    pub size: u32,
    #[serde(default = "default_do_resize")]
    pub do_resize: bool,
    #[serde(default = "default_do_center_crop")]
    pub do_center_crop: bool,
    #[serde(default = "default_crop_size")]
    pub crop_size: u32,
    #[serde(default = "default_do_rescale")]
    pub do_rescale: bool,
    #[serde(default = "default_rescale_factor")]
    pub rescale_factor: f32,
    #[serde(default = "default_do_normalize")]
    pub do_normalize: bool,
    #[serde(default = "default_image_mean")]
    pub image_mean: Vec<f32>,
    #[serde(default = "default_image_std")]
    pub image_std: Vec<f32>,
}

fn default_size() -> u32 {
    224
}

fn default_do_resize() -> bool {
    true
}

fn default_do_center_crop() -> bool {
    true
}

fn default_crop_size() -> u32 {
    224
}

fn default_do_rescale() -> bool {
    true
}

fn default_rescale_factor() -> f32 {
    1.0 / 255.0
}

fn default_do_normalize() -> bool {
    true
}

fn default_image_mean() -> Vec<f32> {
    vec![0.48145466, 0.4578275, 0.40821073]
}

fn default_image_std() -> Vec<f32> {
    vec![0.26862954, 0.2613026, 0.2757771]
}

impl ImageProcessor {
    pub fn from_pretrained(clip_id: &str) -> Result<Self> {
        let api = Api::new().map_err(|e| anyhow::Error::msg(e.to_string()))?;
        let api = api.model(clip_id.to_string());
        let config_filename = api
            .get("preprocessor_config.json")
            .map_err(|e| anyhow::Error::msg(e.to_string()))?;
        let image_processor =
            serde_json::from_slice(&std::fs::read(config_filename).map_err(std::io::Error::from)?)
                .map_err(|e| anyhow::Error::msg(e.to_string()))?;
        Ok(image_processor)
    }

    pub fn preprocess(&self, image: &DynamicImage) -> Result<Tensor> {
        let image = if self.do_resize { self.resize(image) } else { image.clone() };
        let image = if self.do_center_crop { self.center_crop(&image) } else { image };
        let tensor = self.to_tensor(&image)?;
        let tensor = if self.do_rescale { self.rescale(&tensor)? } else { tensor };
        let tensor = if self.do_normalize { self.normalize(&tensor)? } else { tensor };
        self.to_channel_dimension_format(&tensor)
    }

    fn resize(&self, image: &DynamicImage) -> DynamicImage {
        image.clone() // Placeholder
    }

    fn center_crop(&self, image: &DynamicImage) -> DynamicImage {
        image.clone() // Placeholder
    }

    fn to_tensor(&self, image: &DynamicImage) -> Result<Tensor> {
        let img = image.to_rgb8().into_raw();
        let (width, height) = image.dimensions();
        Ok(Tensor::from_vec(img, (height as usize, width as usize, 3), &Device::Cpu)?
            .to_dtype(DType::F32)?)
    }

    fn rescale(&self, tensor: &Tensor) -> Result<Tensor> {
        let rescale_factor = self.rescale_factor as f64;
        Ok(tensor.affine(rescale_factor, 0.0)?)
    }

    fn normalize(&self, tensor: &Tensor) -> Result<Tensor> {
        let image_mean = self.image_mean.clone();
        let image_std = self.image_std.clone();
        let mean = Tensor::from_vec(image_mean, (3,), &Device::Cpu)?;
        let std = Tensor::from_vec(image_std, (3,), &Device::Cpu)?;
        Ok(tensor.broadcast_sub(&mean)?.broadcast_div(&std)?)
    }

    fn to_channel_dimension_format(&self, tensor: &Tensor) -> Result<Tensor> {
        Ok(tensor.permute((2, 0, 1))?)
    }
}

fn main() -> Result<()> {
    let model_path = "llava-hf/llava-v1.6-vicuna-7b-hf".to_string();
    let tokenizer_path = "tokenizer/tokenizer.json".to_string();
    let image_file = "example_image.jpg".to_string();

    let device = Device::cuda_if_available(0)?;

    // Load model, tokenizer, image, and process
    println!("Start loading model");
    let api = Api::new()?.model(model_path.clone());
    let config_filename = api.get("config.json")?;
    let llava_config: LLaVAConfig = serde_json::from_slice(&std::fs::read(config_filename)?)?;
    let _tokenizer = Tokenizer::from_file(&tokenizer_path).map_err(E::msg)?;  // Unused for now

    let image_processor = ImageProcessor::from_pretrained(&llava_config.mm_vision_tower.unwrap())?;
    let img = image::ImageReader::open(&image_file)?.decode()?;
    let img_tensor = image_processor.preprocess(&img)?;
    let _img_tensor = img_tensor.to_device(&device)?;

    println!("Model loaded, image processed.");
    Ok(())
}

The provided code demonstrates how to load and preprocess images using the LLaVA model in Rust, leveraging the candle_core framework for tensor operations. The code is structured into multiple components:

• Conversation struct models a dialogue with customizable separator styles for handling interactions between the user and the assistant.

• ImageProcessor struct is responsible for resizing, cropping, and normalizing image data before transforming it into a tensor suitable for input to the LLaVA model. The image preprocessing pipeline includes resizing the image, applying center cropping, rescaling pixel values, and normalizing them based on predefined mean and standard deviation values.

• The main function coordinates the process by loading the model configuration and tokenizer from the Hugging Face Hub using the hf_hub crate, preprocessing the input image, and converting it into a tensor compatible with the LLaVA model for further tasks, such as visual understanding.

This code illustrates how to work with multi-modal AI models by integrating vision and language processing using Rust. It emphasizes efficient image preprocessing and tensor manipulation in preparation for model inference.

The latest trends in hybrid models and MTL focus on improving the scalability and efficiency of these models. Task-specific adapters and modular neural architectures allow different tasks to share only the relevant parts of the model, reducing the risk of interference between tasks. Meanwhile, low-rank approximation techniques and model pruning are being explored to reduce the computational cost of hybrid models, making them more suitable for deployment in resource-constrained environments.

In conclusion, hybrid models and multi-task learning represent powerful approaches in NLP, enabling models to capture both local and global context and to generalize across multiple tasks. The combination of CNNs, RNNs, and Transformers allows hybrid models to excel in tasks requiring diverse feature extraction, while MTL enables models to share knowledge across related tasks. By implementing these models in Rust, leveraging libraries like tch-rs, NLP practitioners can build efficient, high-performance models that push the boundaries of language understanding and generation.

3.7. Model Explainability and Interpretability link

As neural networks grow increasingly complex, particularly in the field of Natural Language Processing (NLP), the need for model explainability and interpretability has become paramount. These models, including state-of-the-art architectures like Transformers, RNNs, and CNNs, are often seen as "black boxes," making it difficult to understand how they arrive at their predictions. This is particularly concerning in sensitive applications such as healthcare, finance, and legal systems, where the consequences of incorrect or biased predictions can be severe. Model explainability addresses this challenge by providing insights into how a model makes decisions, allowing stakeholders to assess its reliability, fairness, and alignment with ethical standards.

The fundamental idea behind explainability is to make the internal workings of a model transparent. In NLP, this often involves techniques such as attention visualization, feature importance analysis, and gradient-based explanations. Attention mechanisms, particularly in Transformer-based models, offer a natural starting point for interpretability. Since attention mechanisms allocate different weights to different tokens in a sequence, visualizing these weights can provide insights into which parts of the input the model considers most relevant. Mathematically, attention weights are computed as a probability distribution over the input sequence, with each weight indicating the relevance of a specific token. Given an attention matrix $A$ with dimensions $(n, n)$, where $n$ is the sequence length, each element $A_{ij}$ represents how much token $i$ attends to token $j$. Visualizing these weights allows users to see which tokens the model is focusing on during its decision-making process.

For instance, in a sentiment analysis task, attention weights can help identify the specific words or phrases that led the model to classify a sentence as positive or negative. Suppose a sentence like "The movie was incredibly engaging and well-directed" is classified as positive. By visualizing the attention weights, we can see that the model may focus more heavily on the words "engaging" and "well-directed" while downplaying less relevant words like "the" and "was." This kind of transparency is valuable in validating model predictions, especially in tasks where subtle contextual clues significantly influence the outcome.

However, while attention mechanisms provide some level of interpretability, they are not a perfect solution. Transformers are complex models with multiple layers of attention, making it difficult to attribute model decisions to individual layers or heads. Moreover, attention weights can sometimes be misleading, as high attention on a particular word does not necessarily mean that word is the primary driver of the model's decision. This leads to the broader challenge of explaining deep neural networks, where the non-linear interactions between neurons make it difficult to trace how specific inputs are processed to produce outputs.

One approach to improving interpretability is to examine feature importance through gradient-based methods. These methods involve computing the gradient of the model's output with respect to the input features, which provides information about how sensitive the model's predictions are to changes in the input. For example, Integrated Gradients is a popular method that computes the average gradient of the output with respect to the input as the input transitions from a baseline value to its actual value. This approach provides a measure of how important each feature (or word) is to the final prediction. Mathematically, the integrated gradient $IG_i$ for a feature $x_i$ is computed as:

$$ IG_i = (x_i - x'_i) \int_{\alpha=0}^{1} \frac{\partial f(x' + \alpha (x - x'))}{\partial x_i} d\alpha $$

where $x'$ is the baseline input, xxx is the actual input, and $f(x)$ is the model’s output. The integral is approximated by summing the gradients at discrete steps between $x'$ and $x$, providing an importance score for each feature.

Feature importance methods can be particularly useful in NLP applications where certain words or phrases have a disproportionate influence on the model’s decisions. For example, in a toxicity detection model, understanding which words trigger a toxic classification can help model developers ensure that the model is not biased toward certain groups of words or expressions.

In the context of multi-task learning (MTL) models or hybrid models, explainability becomes even more challenging, as these models often involve multiple sub-networks or shared layers. Understanding how information flows between tasks or architectures requires specialized techniques. For instance, layer-wise relevance propagation (LRP) can be used to trace back model decisions through the layers of a neural network, providing insights into how the model’s internal representations evolve at different stages. This technique is particularly useful in understanding how shared representations in multi-task learning models contribute to performance across tasks.

One of the trade-offs between model accuracy and interpretability is that more complex models, such as deep Transformers or hybrid architectures, tend to achieve higher performance but are harder to interpret. Conversely, simpler models, like linear classifiers, are more interpretable but often lack the ability to capture the complexities of natural language. In practice, model developers must balance these two goals—achieving high accuracy while maintaining some level of interpretability. This is especially important in applications like legal document analysis or medical diagnosis, where decisions must be explainable to human experts.

In terms of practical implementation, building tools to visualize attention weights and compute feature importance in Rust can be done using libraries like tch-rs for neural network operations and plotters for visualization. Below is an example of how to visualize attention weights in Rust for a Transformer model using tch-rs:

use tch::{nn, nn::Module, Device, Tensor};

// Dummy function to represent attention weights extraction
fn get_attention_weights(model: &nn::Sequential, input: &Tensor) -> Tensor {
    // Simulating returning attention weights for a given input sequence
    // In reality, you would extract attention from a transformer model.
    model.forward(input)
}

fn visualize_attention(weights: &Tensor) {
    // A simple method to print or visualize attention weights
    println!("Print the Attention Weights: {:?}", weights);
    println!("In Practice, You Can Visualize Attention Weights using Plotters");
}

fn main() -> anyhow::Result<()> {
    let device = Device::cuda_if_available();
    let vs = nn::VarStore::new(device);

    // Define a simple model for demonstration (replace this with a transformer if available)
    let model = nn::seq()
        .add(nn::linear(&vs.root(), 20, 10, Default::default()))
        .add_fn(|xs| xs.relu());

    // Example input (batch of token indices)
    let input = Tensor::randint(100, &[10, 20], (tch::Kind::Int64, device));  // Batch of 10 sequences, each with 20 tokens

    // Ensure the input is converted to the correct dtype, matching the model's parameters
    let input = input.to_kind(tch::Kind::Float);  // Ensure input is of float kind, matching model weights

    // Extract attention weights from the model (using the forward pass as a placeholder)
    let attention_weights = get_attention_weights(&model, &input);

    // Visualize attention weights
    visualize_attention(&attention_weights);

    Ok(())
}

In this code, we assume that the Transformer model has a method to extract attention weights, which can then be visualized using crate like plotters. This type of tool helps in understanding which parts of the input the model focuses on during inference, providing valuable insights into its decision-making process.

Another approach to improving model transparency is through post-hoc explainability techniques, which involve analyzing the model’s outputs and decisions after training. These techniques, such as SHAP (Shapley Additive Explanations) and LIME (Local Interpretable Model-agnostic Explanations), generate explanations for individual predictions by approximating the behavior of the model locally around the input data. These methods are model-agnostic and can be applied to any neural network architecture, making them versatile tools for interpretability.

The latest trends in model explainability focus on creating explanations that are not only accurate but also human-interpretable. This includes developing new methods to simplify complex models without sacrificing performance, as well as designing explainability tools that align with the needs of end-users, such as doctors, lawyers, or business analysts. Moreover, ensuring that explanations are fair and unbiased is an emerging concern, particularly in the context of ethical AI, where models must not only perform well but also operate transparently and equitably.

In conclusion, explainability and interpretability are critical components of deploying NLP models in real-world applications. Techniques like attention visualization, feature importance analysis, and gradient-based explanations help illuminate the inner workings of complex models like Transformers, improving trust and transparency. By implementing these tools in Rust, developers can create NLP systems that are not only powerful but also interpretable, ensuring that their predictions can be understood and trusted by end-users. The challenge moving forward is to strike a balance between high-performance models and the need for clear, actionable explanations, especially as NLP models continue to evolve in complexity.

3.8. Conclusion link

Chapter 3 provides a comprehensive overview of neural network architectures for NLP, from basic principles to cutting-edge models like Transformers and BERT. By integrating theoretical insights with practical Rust implementations, this chapter equips readers with the knowledge and tools needed to develop sophisticated NLP models capable of handling complex language tasks.

3.8.1. Further Learning with GenAI link

These prompts cover a broad range of topics, from fundamental concepts like feedforward networks to advanced architectures such as Transformers, BERT, and GPT. By addressing both theoretical foundations and practical implementations in Rust, these prompts are designed to guide readers toward a comprehensive understanding of how to build, optimize, and interpret neural networks for NLP tasks.

• Explain the limitations of feedforward neural networks in handling sequential data in NLP. How do these limitations motivate the development of more advanced architectures like RNNs and Transformers? Discuss the implications for tasks like language modeling and sentiment analysis.

• Describe the architecture of a simple Recurrent Neural Network (RNN). How does the recurrent connection help in processing sequences? Discuss the challenges of training RNNs, such as vanishing and exploding gradients, and explain how these can be mitigated in Rust.

• Compare Long Short-Term Memory (LSTM) networks with Gated Recurrent Units (GRUs). How do these architectures address the limitations of simple RNNs? Provide a detailed analysis of their internal mechanisms and implement both in Rust for an NLP task.

• Discuss the role of 1D Convolutional Neural Networks (CNNs) in NLP. How do convolutional layers extract local patterns in text, and why are they effective for tasks like text classification? Implement a 1D CNN in Rust and evaluate its performance on a sentiment analysis dataset.

• Explain the concept of self-attention in the Transformer architecture. How does self-attention allow the model to focus on different parts of the input sequence? Provide a step-by-step breakdown of the self-attention mechanism and implement it in Rust.

• What are the key differences between encoder-only, decoder-only, and encoder-decoder Transformer models? Discuss their respective advantages and use cases in NLP, and implement a simple encoder-decoder Transformer model in Rust.

• Analyze the scalability and parallelization advantages of the Transformer architecture compared to RNNs. How do these advantages make Transformers suitable for large-scale NLP tasks like translation and summarization? Implement a Transformer model in Rust and optimize it for performance.

• Discuss the importance of pre-training in models like BERT and GPT. How does the pre-training phase contribute to the model's ability to perform well on downstream tasks? Implement fine-tuning of a pre-trained BERT model in Rust and evaluate its performance on a text classification task.

• Compare the masked language model approach used in BERT with the autoregressive approach used in GPT. How do these differing approaches affect the models' strengths and weaknesses in tasks like text generation and understanding? Implement a small-scale version of both models in Rust and compare their outputs.

• Explain the concept of transfer learning in the context of NLP models like BERT and GPT. How does transfer learning enable these models to achieve state-of-the-art results on a wide range of NLP tasks? Discuss the process of fine-tuning and implement it in Rust.

• Describe the challenges of implementing large-scale pre-trained models like BERT and GPT in Rust. What are the memory and computational considerations, and how can they be addressed in Rust? Explore techniques like model quantization and distillation for optimizing these models.

• How can CNNs, RNNs, and Transformers be combined into a hybrid model for NLP tasks? Discuss the benefits and challenges of such an approach and implement a hybrid model in Rust for a text classification task.

• Explore the concept of multi-task learning in NLP. How does sharing representations across different tasks improve model performance? Implement a multi-task learning model in Rust, using shared and task-specific layers, and evaluate its performance on multiple NLP tasks.

• Discuss the role of attention mechanisms in model interpretability. How can attention weights be used to understand model decisions? Implement tools in Rust to visualize attention weights and use them to analyze model behavior on an NLP task.

• What are the trade-offs between model accuracy and interpretability in neural network architectures for NLP? Discuss how attention mechanisms and feature importance can be balanced with model complexity. Implement methods in Rust to assess these trade-offs in a Transformer model.

• Explain how Transformers handle long-range dependencies in text. Why are they more effective than RNNs in this regard? Implement a Rust-based comparison of an RNN and a Transformer on a task requiring long-range dependency handling, such as document classification.

• Explore the concept of positional encoding in Transformers. Why is it necessary, and how does it allow the model to understand the order of words in a sequence? Implement positional encoding in Rust and analyze its impact on a Transformer model's performance.

• Discuss the significance of bidirectional context in models like BERT. How does bidirectionality contribute to better understanding of language compared to unidirectional models like GPT? Implement a bidirectional Transformer in Rust and compare its performance with a unidirectional one.

• What are the key considerations when implementing model explainability techniques for advanced NLP models like BERT and GPT? Discuss the challenges of interpreting these models and implement methods in Rust to make their predictions more transparent and understandable.

• Analyze the impact of model architecture on the computational efficiency of NLP tasks. Compare the computational requirements of CNNs, RNNs, and Transformers in Rust, focusing on memory usage, training time, and inference speed. Provide a detailed performance analysis and recommendations for optimizing each architecture.

As you engage with these questions, you will not only enhance your understanding of complex architectures like Transformers and BERT but also gain hands-on experience in implementing and optimizing them using Rust.

3.8.2. Hands On Practices link

Self-Exercise 3.1: Implementing and Comparing RNN and Transformer Architectures link

Objective: To understand the differences in handling sequential data between RNNs and Transformers by implementing and comparing both architectures for an NLP task.

Tasks:

• Implement a simple Recurrent Neural Network (RNN) in Rust, designed to handle a sequence-based NLP task, such as sentiment analysis or language modeling.

• Implement a Transformer model for the same NLP task, ensuring it includes key components like self-attention and positional encoding.

• Train both models on the same dataset, ensuring comparable training conditions.

• Analyze and compare the performance of the RNN and Transformer models in terms of accuracy, computational efficiency, and their ability to handle long-range dependencies.

Deliverables:

• Two Rust codebases: one for the RNN implementation and one for the Transformer implementation.

• A detailed comparison report, including performance metrics, training time, and insights into how each architecture handles the given NLP task.

• Visualizations or charts illustrating the performance differences between the two models.

Self-Exercise 3.2: Fine-Tuning a Pre-Trained BERT Model link

Objective: To gain hands-on experience in fine-tuning a pre-trained BERT model for a specific NLP task using Rust.

Tasks:

• Load a pre-trained BERT model and prepare it for fine-tuning on a specific NLP task, such as text classification or named entity recognition.

• Implement the fine-tuning process in Rust, including adapting the BERT model’s architecture for the task at hand.

• Train the fine-tuned model on a labeled dataset, ensuring that you handle issues like overfitting and data imbalance.

• Evaluate the performance of the fine-tuned BERT model on a test set, and compare its results with a baseline model or another pre-trained model.

Deliverables:

• A Rust codebase that includes the fine-tuning implementation of the BERT model.

• A report detailing the fine-tuning process, including the modifications made to the BERT architecture and the training strategy employed.

• An evaluation report comparing the fine-tuned BERT model’s performance with baseline results, including accuracy, precision, recall, and F1-score.

Self-Exercise 3.3: Visualizing Attention Weights in Transformer Models link

Objective: To explore model interpretability by implementing tools for visualizing attention weights in Transformer models applied to NLP tasks.

Tasks:

• Implement a Transformer model for a text-based task, such as machine translation or text summarization, ensuring it includes self-attention mechanisms.

• Develop tools in Rust to visualize the attention weights generated by the Transformer model during inference.

• Apply the visualization tools to interpret the model’s focus on different parts of the input sequence for various test examples.

• Analyze how attention weights correlate with the model’s predictions, and discuss the insights gained from these visualizations in terms of model interpretability and decision-making.

Deliverables:

• A Rust implementation of the Transformer model, with integrated tools for visualizing attention weights.

• A set of visualizations that show attention weights for different input sequences and how they affect the model’s predictions.

• An analysis report discussing the relationship between attention weights and model outputs, including any notable patterns or trends observed.

Self-Exercise 3.4: Implementing a Multi-Task Learning Model for NLP link

Objective: To understand the principles and benefits of multi-task learning by implementing a model that performs multiple NLP tasks simultaneously.

Tasks:

• Design a multi-task learning model in Rust that can handle two or more related NLP tasks, such as text classification and sentiment analysis.

• Implement the model using shared layers for common features and task-specific layers for each individual task.

• Train the multi-task model on a combined dataset, ensuring that each task has sufficient representation in the training process.

• Evaluate the performance of the multi-task model on each task and compare it with single-task models trained separately on the same tasks.

Deliverables:

• A Rust codebase containing the multi-task learning model implementation, including shared and task-specific layers.

• A training report detailing the process and challenges of training a multi-task model.

• An evaluation report comparing the performance of the multi-task model with that of single-task models, including metrics like accuracy, precision, recall, and training efficiency.

Self-Exercise 5.5: Optimizing a Hybrid Model Combining CNNs, RNNs, and Transformers link

Objective: To explore the benefits and challenges of hybrid models by implementing and optimizing a model that combines CNNs, RNNs, and Transformers for an NLP task.

Tasks:

• Design a hybrid model that integrates convolutional layers, recurrent layers, and transformer-based self-attention mechanisms, tailored for a specific NLP task such as text classification or question answering.

• Implement the hybrid model in Rust, ensuring that each component (CNN, RNN, Transformer) is correctly integrated and contributes to the model’s overall performance.

• Train the hybrid model on a large NLP dataset, experimenting with different configurations to find the optimal combination of architectures.

• Compare the hybrid model’s performance with that of individual CNN, RNN, and Transformer models, analyzing both the accuracy and computational efficiency.

Deliverables:

• A Rust codebase implementing the hybrid model, including all necessary components (CNN, RNN, Transformer).

• A detailed training report documenting the experiments conducted, including different architectural configurations and their impact on performance.

• A comprehensive comparison report showing how the hybrid model performs relative to standalone CNN, RNN, and Transformer models, with an analysis of the trade-offs involved.